사용할 모듈 포함문
from sklearn.linear_model import LogisticRegression #로지스틱 회귀
from sklearn.linear_model import LinearRegression #선형 회귀
from sklearn.datasets import load_iris #붓꽃 데이터 로드
from sklearn.model_selection import train_test_split #학습 및 테스트 데이터 분리
from sklearn.metrics import accuracy_score #적합도(분류)
from sklearn.model_selection import cross_val_score #교차 검증 점수
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt다중 분류와 softmax 함수
이진 분류는 참인지 거짓인지 혹은 두 개의 클래스 중에 어디에 속하는지 판별하는 작업입니다.
다중 분류는 두 개 이상의 클래스 중에 어디에 속하는지 판별하는 작업입니다.
다중 분류의 동작은 이진 분류를 클래스 개수만큼 수행한 것을 취합하여 결론을 내립니다.
예를 들어 3개의 클래스(A, B, C)를 갖는 데이터의 다중 분류가 있다고 가정할게요.
다중 분류기 내부에는 3개의 이진 분류기로 구성합니다. 이들은 각각 A 클래스인지 판별, B 클래스인지 판별, C 클래스인지 판별합니다.
그리고 내부 3개의 판별기에 의해 나온 결과를 취합하여 결론을 내립니다.
결론을 내리는 과정에서는 3개의 분류기에 의해 나온 확률의 총 합이 1(100%)로 수렴할 수 있게 수정하는데 이를 softmax라고 부릅니다.
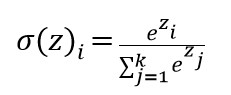
softmax 함수를 코드로 표현하면 다음과 같습니다.
def softmax(y):
for i,e in enumerate(y):
es = np.sum(e)
e = e/es
y[i]=e예를 들어 세 개의 분류기에 의해 나온 결과를 softmax 함수에 의해 최종 결과는 다음처럼 나올 수 있습니다.
y = [[0.01, 0.93, 0.18],
[0.01, 0.92, 0.02],
[0.01, 0.93, 0.14],
[0.01, 0.14, 0.91],
[0.92, 0.09, 0.12],
[0.93, 0.03, 0.01],
[0.89, 0.10, 0.05],
[0.01, 0.91, 0.11],
[0.04, 0.07, 0.92]]
softmax(y)
print(np.round(y,2))[out]
[[0.01 0.83 0.16]
[0.01 0.97 0.02]
[0.01 0.86 0.13]
[0.01 0.13 0.86]
[0.81 0.08 0.11]
[0.96 0.03 0.01]
[0.86 0.1 0.05]
[0.01 0.88 0.11]
[0.04 0.07 0.89]]세 개의 분류기에 의해 나온 결과(A 클래스인지, B클래스인지, C클래스인지)의 총 합이 1이 될 수 있게 하기 위해 다음처럼 결과를 수정합니다.
(A결과/(A결과+B결과+C결과), B결과/(A결과+B결과+C결과), C결과/(A결과+B결과+C결과))
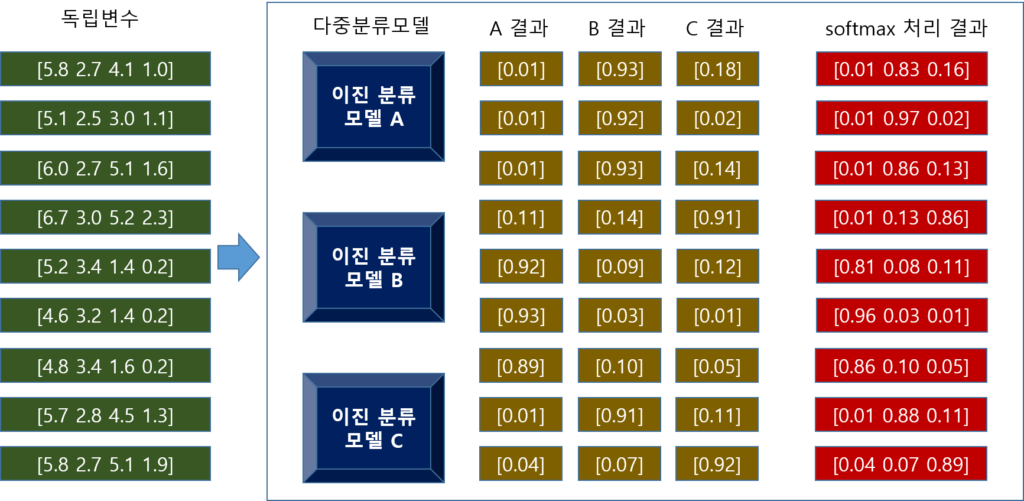
위 그림은 붓꽃 데이터(꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비)를 다중 분류기를 통해 분류하는 과정을 도식한 것입니다. (그림에서 독립 변수 부분 [5.8 2.7 4.1 1.0] …)
여기에서 판단할 붓꽃의 종류는 3종류(setosa, versicolor, virginica)입니다.
따라서 다중 분류기에는 setosa인지 판별, versicolor인지 판별, virginica인지 판별하는 이진 분류기에 의해 판별을 합니다. (그림에서 이진 분류 모델 A, 이진 분류 모델 B, 이진 분류 모델 C)
그리고 판별한 결과(그림에서 A결과, B결과, C결과)를 softmax에 의해 총 합이 1로 수렴할 수 있게 조정한 결과를 도출합니다.( 그림에서 softmax 처리 결과)
이 중에 가장 높은 수치값에 해당하는 클래스로 판별합니다.
다중 분류 모델 만들기
여기에서는 선형 회귀 모델로 다중 분류 모델을 만드는 것을 먼저 실습합시다.
그리고 이진 분류 모델로 다중 분류 모델을 만드는 것을 실습합시다. 실제 다중 분류 모델의 구조는 이 실습이 더 정확하다고 할 수 있겠죠.
마지막으로 사이킷 런에서 제공하는 다중 분류 모델과 비교해 봅시다.
- 선형 회귀 모델로 다중 분류 모델 만들기
먼저 선형 회귀 모델로 다중 분류 모델를 만들어 볼게요. 여기에서는 softmax 함수를 사용하여 최종 결과를 도출하는 부분에 초점을 맞추세요.
선형 회귀 모델로 이진 분류기를 만드는 것은 이전 글인 선형 분류모델에 코드를 그대로 사용할게요.
class BinaryClassifier:
def __init__(self):
self.model = LinearRegression()
def sigmoid(self,x):
return 1/(1+np.exp(-x))
def fit(self,x,y):
y = np.array(y)
y = (y*20)-10 #0은 -10, 1은 10으로 변환
self.model.fit(x,y)
def predict(self,x):
re = self.model.predict(x)
return (self.sigmoid(re)>=0.5).astype(int)
def predict_proba(self,x):
re1 = self.sigmoid(self.model.predict(x))
re2 = 1- re1
return np.stack([re2,re1],axis=1)다중 분류기 클래스 이름을 Classifier1이라고 정할게요.
다중 분류기 내부에는 이진 분류기들로 구성합니다. 이진 분류기를 보관할 리스트를 초기화할게요.
class Classifier1:
def __init__(self):
self.models = []학습하는 fit 메서드에서는 종속 변수의 클래스 개수만큼 이진 분류기를 생성합니다.
그리고 각각의 이진 분류기로 학습합니다. 이에 관한 코드 설명은 이전 글인 선형 분류모델을 참고하세요.
class Classifier1:
def __init__(self):
self.models = []
def fit(self,x,y):
self.models.clear()
unique_y = np.unique(y)
ul = len(unique_y)
self.models = [BinaryClassifier() for _ in range(ul)]
for i in range(ul):
model = self.models[i]
temp_y = (y==i).astype(int) #i번 이면 1, 아니면 0으로 y값을 변환
temp_y = (temp_y*20)-10 #0은 -10, 1은 10으로 변환
model.fit(x,temp_y)내부에 softmax 메서드로 캡슐화할게요.
class Classifier1:
def __init__(self):
self.models = []
def fit(self,x,y):
self.models.clear()
unique_y = np.unique(y)
ul = len(unique_y)
self.models = [BinaryClassifier() for _ in range(ul)]
for i in range(ul):
model = self.models[i]
temp_y = (y==i).astype(int) #i번 이면 1, 아니면 0으로 y값을 변환
temp_y = (temp_y*20)-10 #0은 -10, 1은 10으로 변환
model.fit(x,temp_y)
def softmax(self,y):
for i,e in enumerate(y):
es = np.sum(e)
e = e/es
y[i]=e예측하는 predict 에서는 각 이진 분류기에 의해 나온 결과 중에 제일 큰 값을 낸 값으로 결론을 내립니다.
확률까지 결과로 내 주는 predict_proba 에서는 각각의 이진 분류기에 의해 나온 예측 결과를 취합한 후 softmax 를 수행한 결과를 반환합니다.
class Classifier1:
def __init__(self):
self.models = []
def fit(self,x,y):
self.models.clear()
unique_y = np.unique(y)
ul = len(unique_y)
self.models = [BinaryClassifier() for _ in range(ul)]
for i in range(ul):
model = self.models[i]
temp_y = (y==i).astype(int) #i번 이면 1, 아니면 0으로 y값을 변환
temp_y = (temp_y*20)-10 #0은 -10, 1은 10으로 변환
model.fit(x,temp_y)
def softmax(self,y):
for i,e in enumerate(y):
es = np.sum(e)
e = e/es
y[i]=e
def predict(self,x):
yp = self.predict_proba(x)
return np.array([np.argmax(ype) for ype in yp])
def predict_proba(self,x):
ml = len(self.models)
res = []
for i in range(ml):
model = self.models[i]
res.append(model.predict_proba(x)[:,1])
yp = np.stack([re for re in res],axis=1)
self.softmax(yp)
return yp사용하는 것은 나머지 부분을 구현한 후에 같이 할게요.
- 이진 분류 모델로 다중 분류 모델 만들기
이번에는 이진 분류 모델로 다중 분류 모델을 만드는 것을 해 봅시다.
(여기에서 사용할 이진 분류 모델은 실제로는 다중 분류 모델입니다. 이진 분류 모델이라는 가정하에서 사용할게요.)
클래스 이름은 Classifier2라고 정할게요. 마찬가지로 내부에 이진 분류기를 저장할 리스트를 초기화할게요.
class Classifier2:
def __init__(self):
self.models = []학습하는 fit 메서드에서는 종속 변수의 종류만큼 이진 분류기를 생성합니다.
그리고 각각의 이진 분류기로 학습합니다.
class Classifier2:
def __init__(self):
self.models = []
def fit(self,x,y):
self.models.clear()
unique_y = np.unique(y)
ul = len(unique_y)
self.models = [LogisticRegression() for _ in range(ul)]
for i in range(ul):
model = self.models[i]
temp_y = (y==i).astype(int) #i번 이면 1, 아니면 0으로 y값을 변환
model.fit(x,temp_y)softmax, predict, predict_proba는 앞에서 만든 것과 같습니다.
class Classifier2:
def __init__(self):
self.models = []
def fit(self,x,y):
self.models.clear()
unique_y = np.unique(y)
ul = len(unique_y)
self.models = [LogisticRegression() for _ in range(ul)]
for i in range(ul):
model = self.models[i]
temp_y = (y==i).astype(int) #i번 이면 1, 아니면 0으로 y값을 변환
model.fit(x,temp_y)
def softmax(self,y):
for i,e in enumerate(y):
es = np.sum(e)
e = e/es
y[i]=e
def predict(self,x):
yp = self.predict_proba(x)
return np.array([np.argmax(ype) for ype in yp])
def predict_proba(self,x):
ml = len(self.models)
res = []
for i in range(ml):
model = self.models[i]
res.append(model.predict_proba(x)[:,1])
yp = np.stack([re for re in res],axis=1)
self.softmax(yp)
return yp- 결과 비교하기
이제 실험을 통해 결과를 비교해 봅시다.
먼저 실험에 사용할 붓꽃 데이터를 로딩하여 독립 변수와 종속 변수에 대입합시다.
iris = load_iris()
data = iris.data
target = iris.target학습용 데이터와 테스트 데이터로 분리할게요. (여기에서는 검증 데이터로 분리하는 실험은 생략할게요.)
x_train,x_test, y_train,y_test = train_test_split(data,target)첫 번째 다중 분류 모델(Classifier1)로 실험합시다.
model = Classifier1()
model.fit(x_train,y_train)
pred_train = model.predict(x_train)
pred_test = model.predict(x_test)
print("학습 데이터 적합도:",accuracy_score(y_train,pred_train))
print("테스트 데이터 적합도:",accuracy_score(y_test,pred_test))[out]
학습 데이터 적합도: 0.8303571428571429
테스트 데이터 적합도: 0.8947368421052632학습 데이터의 적합도는 83%, 테스트 데이터의 접합도는 89% 일치하는 것을 알 수 있네요.
이번에는 두 번째 다중 분류 모델(Classifier2)로 실험해 봅시다.
model = Classifier2()
model.fit(x_train,y_train)
pred_train = model.predict(x_train)
pred_test = model.predict(x_test)
print("학습 데이터 적합도:",accuracy_score(y_train,pred_train))
print("테스트 데이터 적합도:",accuracy_score(y_test,pred_test))[out]
학습 데이터 적합도: 0.9375
테스트 데이터 적합도: 0.9736842105263158학습 데이터의 적합도는 94%, 테스트 데이터의 접합도는 97% 일치하는 것을 알 수 있네요.
Classifier1에 비해 많이 나아진 것을 알 수 있네요.
마지막으로 사이킷 런에서 제공하는 다중 분류 모델을 사용해 봅시다.
여기에서는 LogisicRegression을 사용할게요. (Classifier2를 만들 때 이진 분류 모델로 사용했었죠.)
model = LogisticRegression(max_iter=5000)
model.fit(x_train,y_train)
pred_train = model.predict(x_train)
pred_test = model.predict(x_test)
print("학습 데이터 적합도:",accuracy_score(y_train,pred_train))
print("테스트 데이터 적합도:",accuracy_score(y_test,pred_test))[out]
학습 데이터 적합도: 0.9732142857142857
테스트 데이터 적합도: 0.9736842105263158학습 데이터의 적합도는 97%, 테스트 데이터의 접합도는 97% 일치하는 것을 알 수 있네요.
전반적으로 Classifier2와 비슷하네요.
이상으로 다중 분류 모델과 softmax 에 관한 글을 마칠게요.
(참고로 지금 만든 클래스는 이해를 목적으로 만든 것일 뿐 실용적인 목적이 아닙니다. 다른 말로 만들 필요가 1도 없어요.)
