사용할 모듈 포함문
import scipy as sp
from scipy import stats
from scipy.stats import t
import matplotlib.pyplot as plt
import numpy as np
import pandas as pdT 검정
모집단의 분산을 모를 때 표본으로 추정하여 평균의 차이를 알아보는 검정 방법이다.
최대 2개의 집단까지 비교가 가능하다.
T 검정은 다음 조건을 만족할 때 수행할 수 있습니다.
- 연속형 데이터
- 랜덤 표본 데이터
- 모집단의 분포가 정규분포에 유사
- 분산에 동질성이 있다.
T 검정 종류는 다음이 세 가지 방법이 있습니다.
- 1 표본 T검정 – 평균을검정
- 종속 표본 T검정 – 한 집단의 두 개의 데이터의 평균을 비교(데이터 개수가 같음)
- 독립 표본 T검정 – 서로 다른 집단의 데이터의 평균을 비교
1표본 T검정
one sample T Test라고 부릅니다. 예를 통해 알아봅시다.
scipy 모듈의 stats.ttest_1samp 함수를 이용합니다.
scipy.stats.ttest_1samp(a, popmean, axis=0, nan_policy=’propagate’, alternative=’two-sided’, *, keepdims=False) [메뉴얼 바로가기]
과자 A에는 50개의 알사탕이 들어있다고 광고를 하고 있다.
10개의 과자 A를 구입한 후 알사탕 개수를 세 보니 다음과 같았다고 한다.
49, 52, 45, 53, 49, 50, 55, 43, 44, 48
유의수준 0.05에서 광고 유의한 지 검정하시오.
data = np.array([49, 52, 45, 53, 49, 50, 55, 43, 44, 48])
stat,pv = stats.ttest_1samp(data,50)
print(f"양측 검정으로 p-value는 {pv:.3f}")
if pv>0.05:
print("귀무 가설을 기각할 수 없다. 따라서 광고는 유의하다. ")
print("과자 A에는 50개의 알사탕이 들어있다는 것은 타당하다.")
else:
print("귀무 가설을 기각한다. 따라서 광고는 유의하지 않다.")
print("과자 A에는 50개의 알사탕이 들어있다는 것은 타당하지 않다.")[out]
양측 검정으로 p-value는 0.360
귀무 가설을 기각할 수 없다. 따라서 광고는 유의하다.
과자 A에는 50개의 알사탕이 들어있다는 것은 타당하다.시각적으로 확인할 수 있게 좀 더 분석해 볼게요.
scipy 모듈의 stats.t 개체는 자유도를 입력 인자로 생성할 수 있어요.
n = len(data)
df = n-1
t_ = t(df)그리고 ppf 메서드를 통해 원하는 퍼센트 포인트를 구할 수 있습니다. 이를 이용하여 유의 수준 0.05의 저점과 고점을 구하기로 합시다.
양측 검정이므로 ppf메서드에 0.975를 입력하면 상위 0.025 지점의 t값을 확인할 수 있어요.
하위 0.025 지점은 상위 0.025 지점의 t값에 음의 부호를 부여하면 구할 수 있습니다.
다음은 t 검정의 유의수준 α에서의 신뢰구간 추정식입니다.
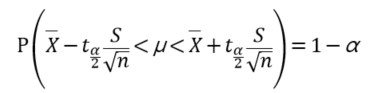
p_05 = t_.ppf(0.975)
data_mean = data.mean()
data_std = data.std(ddof=1)
lp= data_mean - p_05*(data_std/np.sqrt(n))
hp = data_mean + p_05*(data_std/np.sqrt(n))
print(f"유의수준 0.05 [{lp:.4f},{hp:.4f}]")[out]
유의수준 0.05 [45.9826,51.6174]유의수준 0.05에서의 신뢰 구간을 도식화 해 볼게요.
y = t_.pdf(np.arange(-4,4,0.01))
plt.plot(np.arange(-4,4,0.01),y,alpha=0.7,color='r')
y2 = t_.pdf(np.arange(-p_05,p_05,0.01))
plt.fill_between(np.arange(-p_05,p_05,0.01),y2,alpha=0.6,color='b')
plt.title(f"alpha = 0.05 [{lp:.4f},{hp:.4f}]")
plt.show()[out]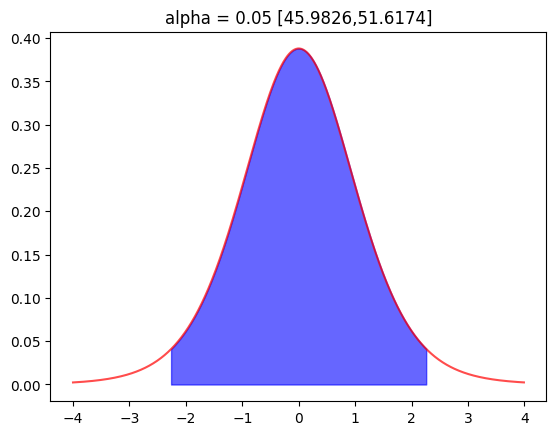
한 가지 예를 더 들어봅시다.
홍길동의 몸무게를 10번 계측을 한 결과는 다음과 같다.
74, 73, 75, 73, 75, 74, 73, 73, 74, 72
신뢰구간 95%(유의수준 0.05)에서 홍길동의 몸무게가 73보다 작다고 할 수 있는지 검정하시오.
이 문제에서는 작은지 검정하는 것이라 단측 검정입니다. 큰 쪽은 확인할 필요가 없죠.
alternative 인자를 ‘less’ 혹은 ‘greater’로 전달하면 단측 검정을 할 수 있습니다.
data = np.array([74, 73, 75, 73, 75, 74, 73, 73, 74, 72])
weight = 73
stat,pv = stats.ttest_1samp(data,weight,alternative='greater')
print(f"단측 검정으로 p-value는 {pv:.4f}")
if pv>=0.05:
print(f"귀무 가설을 기각할 수 없다. 따라서 홍길동의 몸무게는 {weight}보다 크다고 할 수 없다.")
else:
print(f"귀무 가설을 기각한다. 따라서 홍길동의 몸무게는 {weight}보다 크다고 할 수 있다.")[out]
단측 검정으로 p-value는 0.0406
귀무 가설을 기각한다. 따라서 홍길동의 몸무게는 73보다 크다고 할 수 있다.alternative인자를 전달하지 않거나 ‘two-sided’를 전달하면 양측 검정입니다. 이 값을 2로 나누면 단측 검정 결과와 같습니다.
stat,pv = stats.ttest_1samp(data,weight,alternative='two-sided')
print(f"양측 검정일 때 p-value는 {pv:.4f}")[out]
양측 검정일 때 p-value는 0.0811유의수준 0.05에서의 신뢰구간을 구해봅시다.
n = len(data)
df = n-1
t_ = t(df)
data_mean = data.mean()
data_std = data.std(ddof=1)
p_05 = t_.ppf(0.95)
lp= data_mean - p_05*(data_std/np.sqrt(n))
print(f"유의수준 0.05 [,{lp:.4f}]")[out]
유의수준 0.05 [,73.0400]이를 도면화해 봅시다.
y = t_.pdf(np.arange(-4,4,0.01))
plt.plot(np.arange(-4,4,0.01),y,alpha=0.7,color='r')
y2 = t_.pdf(np.arange(-4,-p_05,0.01))
plt.fill_between(np.arange(-4,-p_05,0.01),y2,alpha=0.6,color='b')
plt.text(-p_05-0.5,0.02,"5%")
plt.title(f"alpha = 0.05 [,{lp:.4f}]")
plt.show()[out]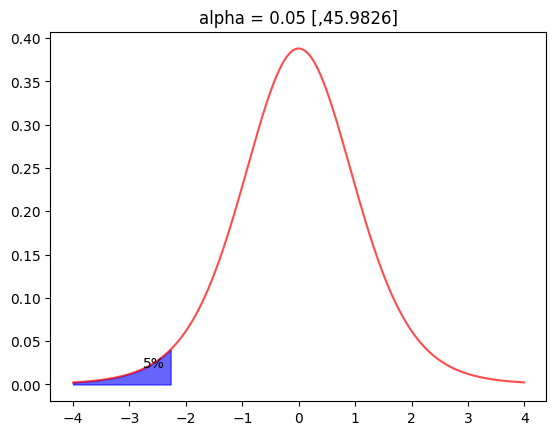
종속 표본 T검정
한 집단의 두 개의 데이터를 비교하는 검정입니다.
특정 실험을 수행하기 전과 후의 차이를 비교할 때 많이 사용합니다.
예를 들어 볼게요.
당뇨 치료제 A를 복용 전 수치와 1달간 복용 후 수치이다.
당뇨 치료제 A를 복용 전과 복용 후에 차이가 있는지 유의수준 0.05에서 검정하시오.
복용 전: 440, 90, 120, 220, 230, 320, 450, 180
복용 후: 220, 80, 100, 110, 180, 250, 350, 170
ttest_1samp 함수를 이용하고자 한다면 비교할 두 개의 데이터의 차이를 입력 인자로 전달합니다.
data_a = np.array([440, 90, 120, 220, 230, 320, 450, 180])
data_b = np.array([220, 80, 100, 110, 180, 250, 350, 170])
diff = data_b - data_a
stat,pv = stats.ttest_1samp(diff,0)
print(f"양측 검정으로 p-value는 {pv:.3f}")
if pv>0.05:
print("귀무 가설을 기각할 수 없다. 따라서 치료제는 유의하지 않다. ")
else:
print("귀무 가설을 기각한다. 따라서 치료제는 유의하다.")[out]
양측 검정으로 p-value는 0.021
귀무 가설을 기각한다. 따라서 치료제는 유의하다.scipy 모듈의 stats.ttest_rel 함수를 이용할 수도 있습니다. (실제 이 목적의 함수입니다.)
scipy.stats.ttest_rel(a, b, axis=0, nan_policy=’propagate’, alternative=’two-sided’, *, keepdims=False) [메뉴얼 바로가기]
data_a = np.array([440, 90, 120, 220, 230, 320, 450, 180])
data_b = np.array([220, 80, 100, 110, 180, 250, 350, 170])
diff = data_b - data_a
stat,pv = stats.ttest_rel(data_a,data_b,alternative='two-sided')
print(f"양측 검정으로 p-value는 {pv:.3f}")
if pv>0.05:
print("귀무 가설을 기각할 수 없다. 따라서 치료제는 유의하지 않다. ")
else:
print("귀무 가설을 기각한다. 따라서 치료제는 유의하다.")[out]
양측 검정으로 p-value는 0.021
귀무 가설을 기각한다. 따라서 치료제는 유의하다.비슷한 문제이지만 단측 검정을 요구하는 문제일 수도 있습니다.
다음은 단측 검정을 요구하는 예입니다.
당뇨 치료제 A를 복용 전 수치와 1달간 복용 후 수치이다.
당뇨 치료제 A를 복용 후에 당뇨 수치를 낮추는 효과가 있는지 유의 수준 0.05에서 검정하시오.
복용 전: 440, 90, 120, 220, 230, 320, 450, 180
복용 후: 220, 80, 100, 110, 180, 250, 350, 170
data_a = np.array([440, 90, 120, 220, 230, 320, 450, 180])
data_b = np.array([220, 80, 100, 110, 180, 250, 350, 170])
diff = data_b - data_a
stat,pv = stats.ttest_rel(data_a,data_b,alternative='greater') #치료 전이 더 큰지(치료 후가 더 작은지)
print(f"단측 검정으로 p-value는 {pv:.3f}")
if pv>0.05:
print("귀무 가설을 기각할 수 없다. 따라서 치료제는 유의하지 않다. ")
else:
print("귀무 가설을 기각한다. 따라서 치료제는 유의하다.")[out]
단측 검정으로 p-value는 0.011
귀무 가설을 기각한다. 따라서 치료제는 유의하다.독립 표본 T검정
서로 다른 두 그룹의 평균이 같은지 검정하는 도구입니다.
‘2집단 t검정’ 혹은 ‘2표본 t검정’으로도 부릅니다.
예를 들어 확인해 볼게요.
A, B 두 그룹의 학생 성적이 있다.
그룹에 따라 성적에 차이가 있는지 유의수준 0.05에서 검정하시오.
A 그룹 성적: 90, 87, 74, 85, 98, 82
B 그룹: 85, 92, 72, 86
독립 표본 t검정에 사용할 함수는 scipy 모듈의 stats.ttest_ind입니다.
scipy.stats.ttest_ind(a, b, axis=0, equal_var=True, nan_policy=’propagate’, permutations=None, random_state=None, alternative=’two-sided’, trim=0, *, keepdims=False)[메뉴얼 바로가기]
data_a = np.array([90, 87, 74, 85, 98, 82])
data_b = np.array([85, 92, 72, 86])
stat, pvalue = stats.ttest_ind(data_a,data_b)
print(f"양측 검정으로 p-value는 {pvalue:.4f}")
if pv>0.05:
print("귀무 가설을 기각할 수 없다. 따라서 두 그룹의 성적은 차이가 있다고 할 수 없다.")
else:
print("귀무 가설을 기각한다. 따라서 두 그룹의 성적은 차이가 있다고 할 수 있다.")[out]
양측 검정으로 p-value는 0.681
귀무 가설을 기각할 수 없다. 따라서 두 그룹의 성적은 차이가 있다고 할 수 없다.데이터만 다른 같은 예입니다.
A, B 두 그룹의 학생 성적이 있다.
그룹에 따라 성적에 차이가 있는지 유의수준 0.05에서 검정하시오.
A 그룹 성적: 90, 87, 74, 85, 98, 82
B 그룹 성적: 56, 65, 77, 80
data_a = np.array([90, 87, 74, 85, 98, 82])
data_b = np.array([56, 65, 77, 80])
stat, pvalue = stats.ttest_ind(data_a,data_b)
print(f"양측 검정으로 p-value는 {pvalue:.4f}")
if pv>0.05:
print("귀무 가설을 기각할 수 없다. 따라서 두 그룹의 성적은 차이가 있다고 할 수 없다.")
else:
print("귀무 가설을 기각한다. 따라서 두 그룹의 성적은 차이가 있다고 할 수 있다.")[out]
양측 검정으로 p-value는 0.0250
귀무 가설을 기각할 수 없다. 따라서 두 그룹의 성적은 차이가 있다고 할 수 없다.또 다른 예를 하나 더 들어볼게요.
다음은 대학교 졸업 여부에 따른 두 그룹의 연봉이다.
대학교 졸업하였을 때 연봉이 더 높다고 할 수 있는지 유의수준 0.05에서 검정하시오.
졸업 O: 4000, 3500, 6000, 8000, 5500, 4300
졸업 X: 4000, 3800, 4200, 3600, 5200, 6000
data_a = np.array([4000, 3500, 6000, 8000, 5500, 4300])
data_b = np.array([4000, 3800, 4200, 3600, 5200, 6000])
stat, pvalue = stats.ttest_ind(data_a,data_b,alternative='greater')
print(f"단측 검정으로 p-value는 {pvalue:.4f}")
if pvalue>=0.05:
print(f"귀무 가설을 기각할 수 없다. 따라서 대학교 졸업한 사람의 연봉이 더 많다고 볼 수 없다.")
else:
print(f"귀무 가설을 기각한다. 따라서 대학교 졸업한 사람의 연봉이 더 많다고 볼 수 있다.")[out]
단측 검정으로 p-value는 0.1784
귀무 가설을 기각할 수 없다. 따라서 대학교 졸업한 사람의 연봉이 더 많다고 볼 수 없다.