사용할 모듈 포함문
import scipy as sp
from scipy import stats
from scipy.stats import poisson #포아송분포
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd포아송분포 (POISSON)
포아송분포는 단위 시간 내에 어떤 사건이 발생할 횟수의 분포입니다.
횟수의 분포여서 이산 확률 분포이며 연속 확률 분포가 아닙니다.
포아송 분포를 다룰 때 지수분포도 함께 소개하는 곳이 많습니다.
포아송분포가 사건이 발생할 횟수의 분포라면 지수분포는 다음 사건이 발생할 때까지 대기시간의 분포입니다. (지수분포는 연속 확률 분포입니다.)
포아송분포의 전제 조건
- 발생한 어떤 사건은 다른 시간 혹은 공간에서 발생한 사건과 서로 독립이다.
- 단위 시간이나 단위 공간에서 발생한 평균 발생 횟수는 일정하다.
- 매우 짧은 시간 혹은 매우 작은 공간에서 두 개 이상의 사건이 발생할 확률은 0에 가깝다.
포아송분포 샘플 생성
scipy 모듈의 stats.poisson 에서도 샘플 생성(rvs), 확률 질량 함수(pmf), 누적 분포 함수(cdf), 생존 함수(sf), 퍼센트 포인트 함수(ppf) 등을 제공합니다. [메뉴얼 바로 가기]
예를 통해 이들 함수 사용해 봅시다.
A제품은 하루에 5개의 불량이 나온다고 한다. 이에 관한 100일간의 샘플을 생성하시오.
y = poisson.rvs(mu=5,size=100)
print(y)[out]
[ 6 7 4 5 3 3 3 3 7 5 6 2 4 5 1 2 6 3 6 7 4 8 6 3
4 5 3 3 3 3 2 7 6 3 7 2 2 4 5 6 4 3 6 7 9 9 7 2
6 5 8 7 6 4 6 3 4 4 5 4 5 7 3 5 8 6 2 11 7 4 5 7
9 3 8 8 4 5 4 5 2 7 4 10 4 2 8 5 3 2 9 4 8 8 8 6
7 4 9 3]이를 히스토그램으로 도식화합시다.
plt.hist(y,bins=range(0,15))
plt.title('mu=5, size=100')
plt.show()[out]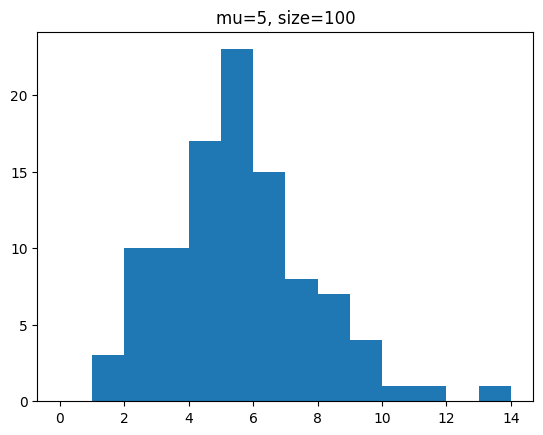
단위 시간에 평균 1회 발생하는 사건을 샘플 개수를 100, 1000, 100000 개일 때 분포를 확인해 봅시다.
for s in [100,1000,100000]:
y = poisson.rvs(mu=1,size=s)
plt.hist(y,bins=range(0,15))
plt.title(f'mu=1, size={s}')
plt.show()[out]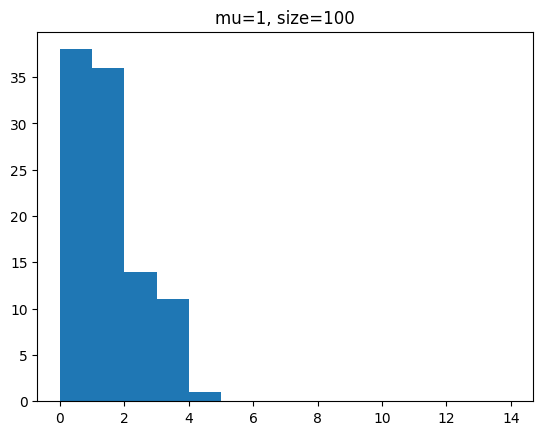
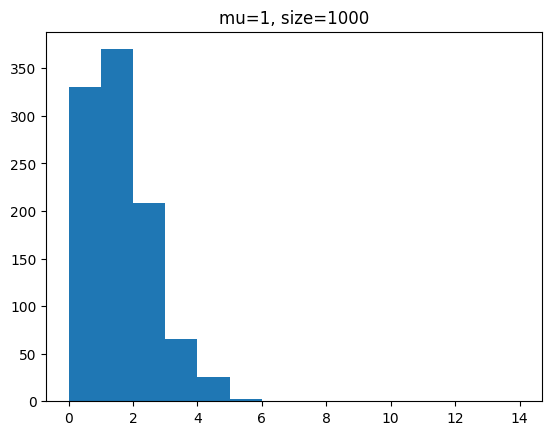
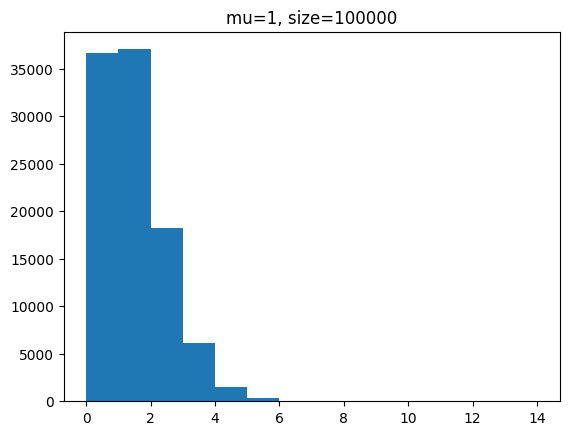
단위 시간에 평균 3회 발생하는 사건을 샘플 개수를 100, 1000, 100000 개일 때 분포를 확인해 봅시다.
for s in [100,1000,100000]:
y = poisson.rvs(mu=3,size=s)
plt.hist(y,bins=range(0,15))
plt.title(f'mu=3, size={s}')
plt.show()[out]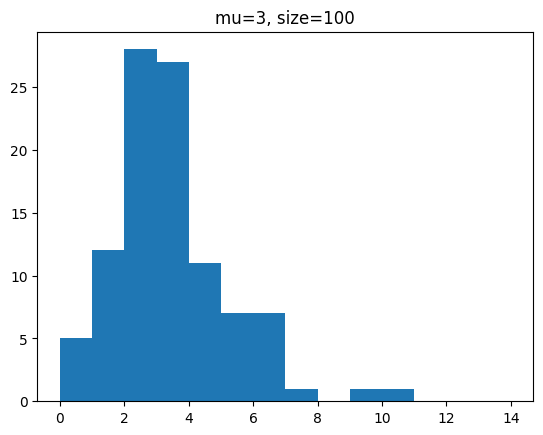
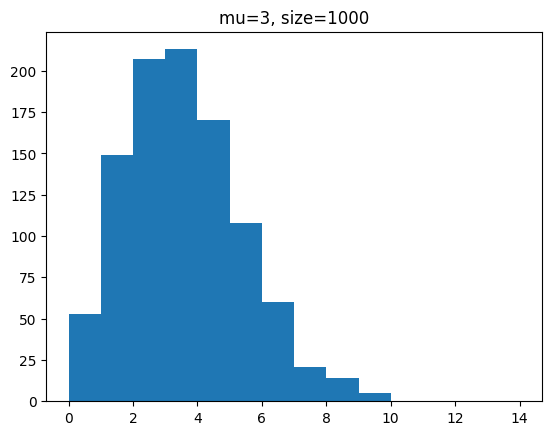
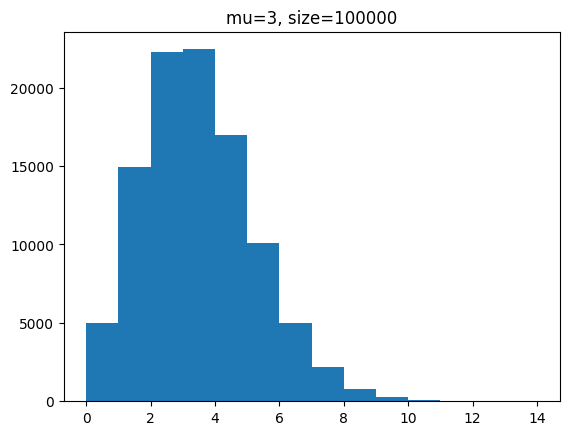
사건 발생 횟수에 따른 분포를 샘플을 통해 확인해 보았습니다.
포아송분포 확률 질량 함수
이번에는 앞에서 확인했던 분포를 공식화하여 제공하는 확률 질량 함수를 사용해서 도식화해 보기로 할게요.
여기에서는 단위 시간에 발생할 사건 평균 횟수가 1, 2, 5, 10일 때 확률 질량 함수를 이용하여 도식화할게요.
bins=range(0,15)
ls = ['-','--','-.',':']
for i,mu in enumerate([1,2,5,10]):
y = poisson.pmf(mu=mu,k=bins)
plt.plot(bins,y,linestyle=ls[i],label=f'mu={mu}')
plt.legend()
plt.show()[out]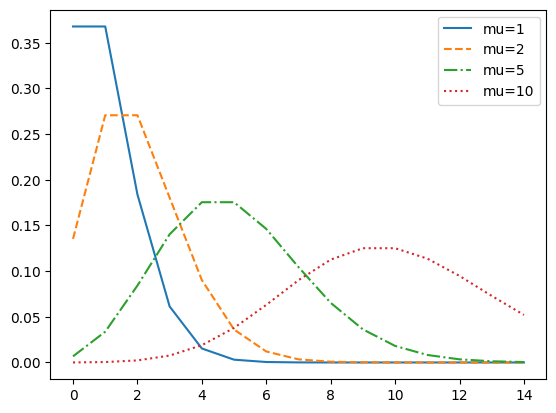
포아송분포의 누적 확률 분포 함수
이번에는 예를 통해 누적 확률 분포 함수인 cdf를 사용해 보기로 할게요.
2022년 기준으로 한 시간 평균 신생아 수는 682명이라고 한다.
한 시간에 650명 이하의 신생아를 낳을 확률을 구하시오.
먼저 확률 질량 함수로 0명에서 650명 낳을 확률의 합을 계산해 볼게요.
s=0
for i in range(650+1):
s += poisson.pmf(mu=682,k=i)
print(s)[out]
0.11328673711428999이를 누적 확률 분포 cdf 함수를 사용하면 한 번의 호출로 알 수 있습니다.
p = poisson.cdf(mu=682,k=650)
print(p)[out]
0.11328673711427531하루에 630명 미만의 신생아를 낳을 확률을 구하시오.
포아송분포는 연속 확률 분포가 아닌 이산 확률 분포입니다. 따라서 630명 미만이라는 것은 629 이하와 같습니다.
p = poisson.cdf(mu=682,k=629)
print(p)[out]
0.021151977250851533이를 개략적으로 도식화해 볼게요. (코드 설명은 생략할게요.)
x=range(500,800)
y = poisson.pmf(mu=682,k=x)
plt.plot(x,y,alpha=0.7,label='pmf')
x2 = range(500,630)
y2 = poisson.pmf(mu=682,k=x2)
plt.fill_between(x2,y2,color='r',label='x<630') #630명 미만일 때 확률(면적)
x3 = range(630,651)
y3 = poisson.pmf(mu=682,k=x3)
plt.fill_between(x3,y3,color='c',label='630<x<=651') #630명 이상 650명 이하일 때 확률(면적)
plt.xticks([500,630,650,682,800])
plt.title("")
plt.show()[out]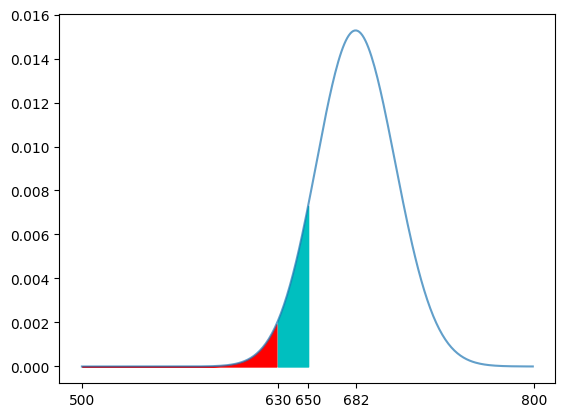
앞에서 이하와 미만일 때의 확률 계산을 했습니다. 이번에는 초과와 이상을 해 보기로 할게요.
하루에 700명을 초과하여 신생아를 낳을 확률을 구하시오.
먼저 확률 질량 함수 pmf를 이용해서 코드를 작성해 봅시다.
전체 확률 1에서 0명~700명일 확률을 빼 줍니다.
p = 1
for i in range(701):
p -= poisson.pmf(mu=682,k=i)
print(p)[out]
0.238359618429192451 – cdf 호출 결과로 알아낼 수도 있습니다.
p = 1 - poisson.cdf(mu=682,k=700)
print(p)[out]
0.23835961842930475sf 함수를 호출해서 알아낼 수도 있습니다.
p = poisson.sf(mu=682,k=700)
print(p)[out]
0.23835961842930484하루에 700명 이상의 신생아를 낳을 확률을 구하시오.
이상의 확률을 구할 때 cdf나 sf 함수의 k인자로 1 작은 값을 전달해야 합니다.
위 예에서 0명에서 699명일 확률을 빼 주면 700명 이상의 확률을 구할 수 있기 때문입니다.
p = 1 - poisson.cdf(mu=682,k=699)
print(p)[out]
0.2502732528118701sf 함수를 이용한 코드입니다.
p = poisson.sf(mu=682,k=699)
print(p)[out]
0.25027325281187포아송분포의 퍼센트 포인트 함수
특정 확률에 속하는 사건 횟수를 구할 수도 있습니다. 예를 들어 알아볼게요.
하루에 n명 이하의 신생아가 낳을 확률은 처음으로 80%가 넘는다고 한다. n을 구하시오.
n = poisson.ppf(q=0.8, mu=682)
print(n)[out]
704.0703명 이하일 확률과 704명 이하일 확률은 다음과 같습니다.
p1 = poisson.cdf(mu=682,k=703)
print("703명 이하일 확률:",p1)
p2 = poisson.cdf(mu=682,k=704)
print("704명 이하일 확률:",p2)[out]
703명 이하일 확률: 0.7954157446153893
704명 이하일 확률: 0.8059984974302791이를 보면 알 수 있듯이 704명 이하로 태어날 확률은 처음으로 80%를 넘는다는 것을 알 수 있습니다.
주의
모든 사건의 발생 횟수가 포아송분포를 따르는 것은 아닙니다. 앞에서 세 가지 전제 조건에 해당해야 포아송분포를 따릅니다. 다음은 포아송 분포를 따르지 않는 사건입니다.
한 시간에 회사에 들어오는 인원은 포아송분포가 아닙니다. (시간 대에 따라 인원 수의 평균은 다릅니다.)
