사용할 모듈 포함문
import scipy as sp
from scipy import stats
from scipy.stats import expon #지수분포
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd지수분포
포아송분포를 따르는 사건이 있을 때 사건 발생까지의 대기시간 분포를 지수분포라고 합니다.
포아송분포는 단위 시간 내에 사건이 발생할 횟수의 분포입니다.(이산 확률 분포)
지수분포는 다음 사건이 일어날 때까지 대기시간의 분포입니다. (연속 확률 분포로 전제 조건이 사건 분포가 포아송분포를 따를 때)
scipy 모듈에서는 stats.expon에서 샘플 생성(rvs), 확률 밀도 함수(pdf), 누적 분포 함수(cdf), 생존 함수(sf), 퍼센트 포인트 함수(ppf) 등을 제공합니다. [메뉴얼 사이트 바로가기]
지수분포 샘플 생성
예를 통해 지수분포 관련 함수들을 사용해 봅시다.
A스마트 폰의 배터리 수명은 평균 24시간이라고 한다.
A스마트 폰 샘플을 100개 생성하시오.
샘플 생성 함수는 rvs 함수입니다.
sample = expon.rvs(scale=24,size=100)
print(np.round(sample,2))[out]
[ 90.77 38.91 25.08 70.13 71.44 58.93 19.55 4.1 5.57 12.8
50.99 37.41 16.25 22.1 8.26 30.16 0.41 21.99 7.53 2.73
33.79 1.25 7.62 4.34 2.77 12.65 15.87 22.55 14.41 105.68
54.74 15.83 7.1 38.64 1.01 44.09 45.67 20.24 8.4 3.27
13.06 26.9 27.84 5.55 0.17 8.78 4.73 9.93 46.16 49.86
3.28 4.7 28.95 29.19 6.37 2.6 32.67 22.34 17.56 8.6
4.18 9.2 47.96 13.39 11.27 2.07 55.85 22.04 17.82 44.72
46.11 12.68 49.31 4.91 6.58 85.83 16.65 29.54 35.64 1.98
2.16 2.73 7.19 84.76 14.13 31.15 14.01 11.91 11.02 39.32
23.09 20.39 9.62 21.29 22.11 7.78 4.42 2.73 11.52 4.53]분포를 히스토그램으로 확인해 봅시다.
lp = int(sample.min())-1
hp = int(sample.max())+1
plt.hist(sample,bins=range(lp,hp))
plt.title('expon.rvs(scale=24,size=100)')
plt.show()[out]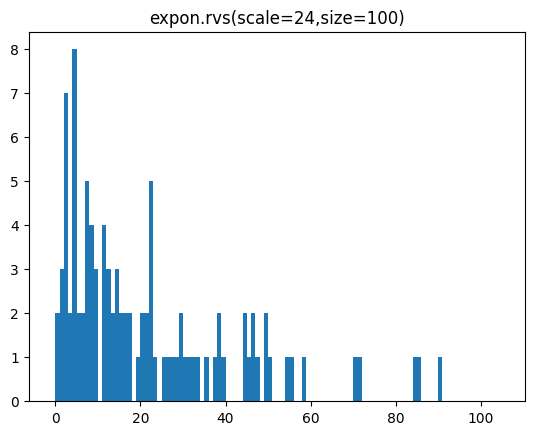
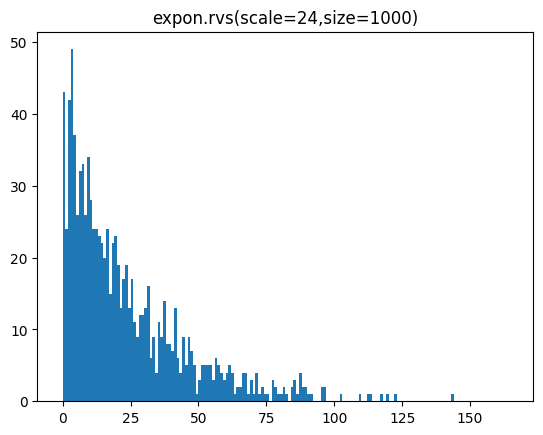
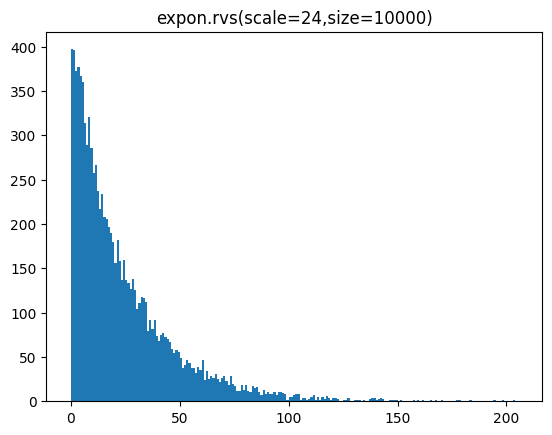
샘플 개수를 100개, 1000개, 10000개일 때 분포를 히스토그램으로 표시해 봅시다.
for s in [100,1000,10000]:
sample = expon.rvs(scale=24,size=s)
lp = int(sample.min())-1
hp = int(sample.max())+1
plt.hist(sample,bins=range(lp,hp))
plt.title(f'expon.rvs(scale=24,size={s})')
plt.show()[out]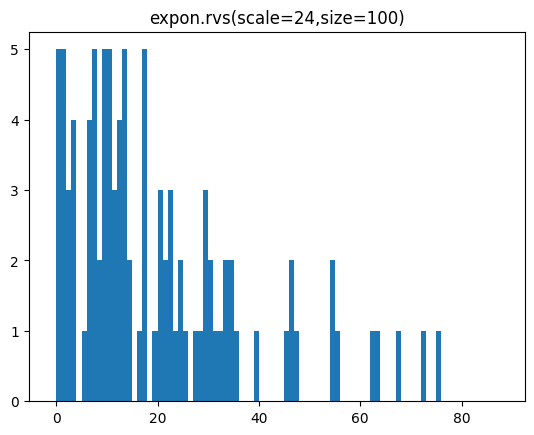
지수분포의 확률 밀도 함수
확률 밀도 함수는 pdf 함수입니다. 예를 통해 확인해 봅시다.
A스마트 폰의 배터리 수명은 평균 24시간이라고 한다.
A스마트 폰 배터리가 소진할 시간별 확률을 구하시오.
x = range(0,100)
y = expon.pdf(scale=24,x=x)
for i in x:
print(f'{i:02d}시간 {y[i]:.2f}', end=' ')
if i%10==9:
print()[out]
00시간 0.04 01시간 0.04 02시간 0.04 03시간 0.04 04시간 0.04 05시간 0.03 06시간 0.03 07시간 0.03 08시간 0.03 09시간 0.03
10시간 0.03 11시간 0.03 12시간 0.03 13시간 0.02 14시간 0.02 15시간 0.02 16시간 0.02 17시간 0.02 18시간 0.02 19시간 0.02
20시간 0.02 21시간 0.02 22시간 0.02 23시간 0.02 24시간 0.02 25시간 0.01 26시간 0.01 27시간 0.01 28시간 0.01 29시간 0.01
30시간 0.01 31시간 0.01 32시간 0.01 33시간 0.01 34시간 0.01 35시간 0.01 36시간 0.01 37시간 0.01 38시간 0.01 39시간 0.01
40시간 0.01 41시간 0.01 42시간 0.01 43시간 0.01 44시간 0.01 45시간 0.01 46시간 0.01 47시간 0.01 48시간 0.01 49시간 0.01
50시간 0.01 51시간 0.00 52시간 0.00 53시간 0.00 54시간 0.00 55시간 0.00 56시간 0.00 57시간 0.00 58시간 0.00 59시간 0.00
60시간 0.00 61시간 0.00 62시간 0.00 63시간 0.00 64시간 0.00 65시간 0.00 66시간 0.00 67시간 0.00 68시간 0.00 69시간 0.00
70시간 0.00 71시간 0.00 72시간 0.00 73시간 0.00 74시간 0.00 75시간 0.00 76시간 0.00 77시간 0.00 78시간 0.00 79시간 0.00
80시간 0.00 81시간 0.00 82시간 0.00 83시간 0.00 84시간 0.00 85시간 0.00 86시간 0.00 87시간 0.00 88시간 0.00 89시간 0.00
90시간 0.00 91시간 0.00 92시간 0.00 93시간 0.00 94시간 0.00 95시간 0.00 96시간 0.00 97시간 0.00 98시간 0.00 99시간 0.00 이를 도면으로 시각화합시다.
plt.plot(x,y)
plt.xlabel("time")
plt.ylabel("probability")
plt.show()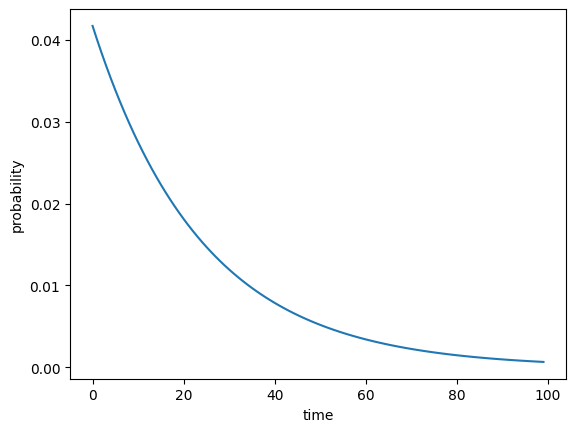
다음은 사건 발생 대기 시간이 1, 2, 5인 지수 분포의 pdf 함수 호출 결과를 시각화한 것입니다.
x = np.arange(0,10,0.1)
ls =['-','--','-.']
for i,s in enumerate([1,2,5]):
y = expon.pdf(scale=s,x=x)
plt.plot(x,y,linestyle=ls[i],label=f'expon.pdf(scale={s},x=x)')
plt.xlabel("time")
plt.ylabel("probability")
plt.legend()
plt.show()[out]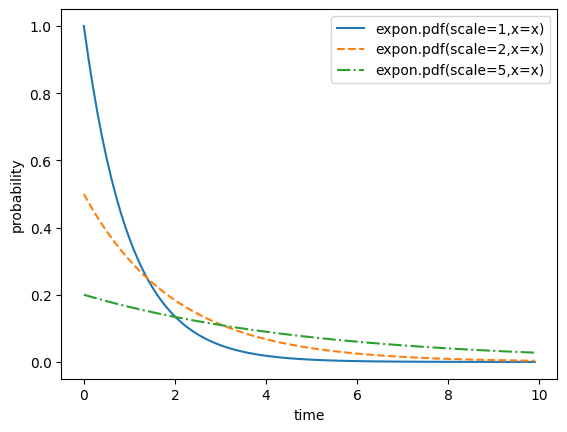
지수분포의 누적 밀도 함수
지수분포의 누적 밀도 함수는 cdf입니다. 예를 통해 사용 해 봅시다.
A스마트 폰의 배터리 수명은 평균 24시간이라고 한다.
A스마트 폰 배터리가 20시간 이내에 소진할 확률을 소수점 이하 2자리까지 구하시오.
p = expon.cdf(scale=24,x=20)
pp = round(p*100,2)
print(pp,"%")[out]
56.54 %A스마트 폰의 배터리 수명은 평균 24시간이라고 한다.
A스마트 폰 배터리가 12시간 이상 36시간 이내에 소진할 확률을 소수점 이하 2자리까지 구하시오.
lp = expon.cdf(scale=24,x=12)
hp = expon.cdf(scale=24,x=36)
pp = round((hp-lp)*100,2)
print(pp,"%")[out]
38.34 %사건 발생 대기 시간이 1, 2, 5일 때 누적 밀도 함수 호출 결과를 시각화해 봅시다.
x = np.arange(0,10,0.1)
ls =['-','--','-.']
for i,s in enumerate([1,2,5]):
y = expon.cdf(scale=s,x=x)
plt.plot(x,y,linestyle=ls[i],label=f'expon.cdf(scale={s},x=x)')
plt.xlabel("time")
plt.ylabel("probability")
plt.legend()
plt.show()[out]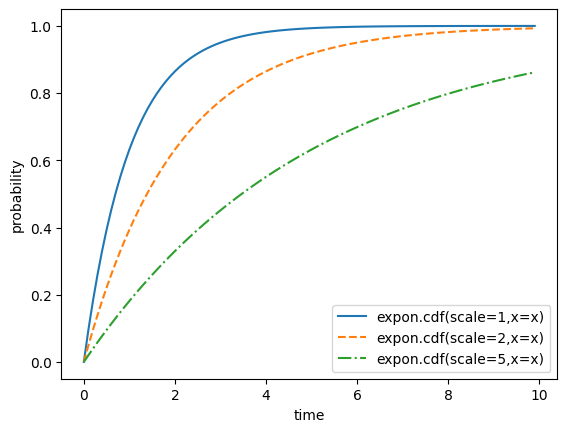
지수분포의 생존 함수
지수분포의 생존 함수는 sf입니다. 이는 1 -cdf 함수 호출 결과와 같습니다. 예를 통해 사용해 봅시다.
A스마트 폰의 배터리 수명은 평균 24시간이라고 한다.
A스마트 폰 배터리가 30시간이 지나도 소진하지 않을 확률을 소수점 이하 2자리까지 구하시오.
p = expon.cdf(scale=24,x=30)
pp = round((1-p)*100,2)
print(pp,"%")[out]
28.65 %p = expon.sf(scale=24,x=30)
pp = round(p*100,2)
print(pp,"%")[out]
28.65 %지수분포의 퍼센트 포인트 함수
지수분포의 퍼센트 포인트 함수는 ppf입니다. 예를 통해 사용해 봅시다.
A스마트 폰의 배터리 수명은 평균 24시간이라고 한다.
A스마트 폰 배터리가 n시간까지 소진할 확률이 85%라고 한다.
n시간을 구하시오.(소수점 이하 2자리까지 계산)
n = expon.ppf(scale=24,q=0.85)
print(round(n,2),"시간")[out]
45.53 시간A스마트 폰의 배터리 수명은 평균 24시간이라고 한다.
A스마트 폰 배터리가 n시간까지 소진하지 않을 확률이 85%라고 한다.
n시간을 구하시오.(소수점 이하 2자리까지 계산)
n = expon.ppf(scale=24,q=(1-0.85))
print(round(n,2),"시간")[out]
3.9 시간확률에 따른 대기 시간을 시각적으로 나타내 봅시다.
x = np.arange(0,1,0.05)
y = expon.ppf(scale=24,q=x)
plt.plot(x,y,label=f'expon.ppf(scale=24)')
plt.xlabel("probability")
plt.ylabel("time")
plt.legend()
plt.show()[out]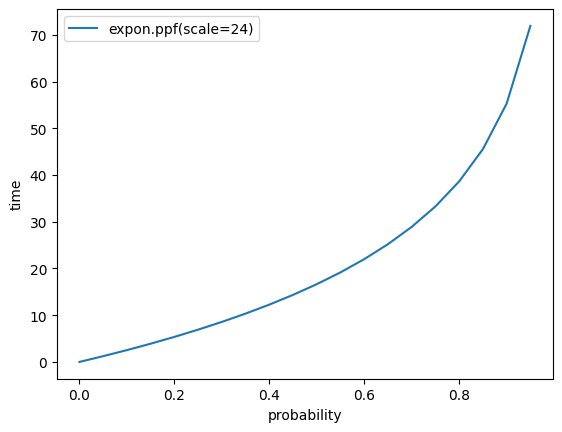
cdf 함수는 입력 인자가 대기 시간이고 출력은 확률입니다.
ppf함수는 입력 인자는 확률이고 출력은 대기 시간입니다.
p = expon.cdf(scale=24,x=24)
print(p)[out]
6321205588285577y = expon.ppf(scale=24,q=p)
print(y)[out]
24.0