[카테고리:] <span>파이썬으로 다루는 통계</span>

사용할 모듈 포함문

import scipy as sp
from scipy import stats
from scipy.stats import f #F분포
from scipy.stats import chi2 #카이제곱분포
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

F분포

F분포는 카이제곱분포를 따르는 두 개의 분포가 있을 때 두 개의 분산 비율을 비교하기 위한 분포입니다.

F분포를 설명하기 위해 가정을 할게요.

카이제곱분포를 따르는 두 개의 분포가 A,B라고 하고 자유도를 a,b라고 합시다.

A 분포의 표본을 X1, B표본의 샘플을 X2라고 할 때 F분포는 (X1/a)/(X2/b)의 분포입니다.

scipy 모듈에서는 stats.f에서 다양한 함수를 제공합니다. [메뉴얼 사이트 바로가기]

F분포의 샘플 생성

F분포를 따르는 샘플을 생성하는 함수는 rvs입니다.

rvs(dfn, dfd, loc=0, scale=1, size=1, random_state=None)

두 개의 샘플의 자유도를 dfn과 dfd로 전달하고 생성할 샘플 개수를 size로 전달합니다.

카이제곱분포를 따르는 두 개의 샘플의 자유도가 5, 7 일 때 F분포 샘플을 100개 만들는 코드는 다음과 같습니다.

sample = f.rvs(dfn=5,dfd=7,size=100)
print(sample)

[out]
[2.62600381 1.60337962 1.55017751 1.15858907 0.14570837 1.62978651
 1.36743155 1.66963104 1.80218564 0.49145854 3.56085621 1.37489861
 0.95536242 0.83700464 0.20497699 0.40970639 3.70819578 2.2783963
 0.35821819 0.86482416 3.91160418 1.06727053 1.44872377 0.68247005
 0.88096718 1.2557473  0.83340679 0.92973642 0.45467542 0.43327642
 0.68269401 1.23657828 1.29944727 0.82686232 1.97173864 0.36814817
 1.88081733 0.45097023 1.16362747 1.02905303 0.54337998 2.03138068
 0.29530759 1.0999222  1.26105966 0.5041756  0.67363905 1.35584471
 0.76596062 0.58368238 2.34178516 0.34796832 1.27878929 2.51584067
 1.561901   0.96765528 1.65810946 0.64980389 0.79729748 0.15351174
 0.9216806  3.14893193 1.658196   0.58729871 0.52209482 0.65376967
 0.53279876 1.91078218 0.61193385 2.01349602 1.29090102 1.67271344
 0.13948061 0.47997901 0.75215119 0.7370377  0.81775238 1.2418709
 2.71860808 1.57447799 0.63376674 2.69898809 0.71001588 0.78604676
 1.48633537 1.01629669 1.58611377 4.09442384 1.61712783 0.50932476
 1.87986909 3.19176189 0.48456451 0.95789392 2.1402151  0.86421057
 0.58425616 0.60457436 0.69900545 1.09971875]

분포를 히스토그램으로 시각화해 봅시다.

plt.hist(sample)
plt.title('f.rvs(dfn=5,dfd=7,size=100)')
plt.show()

[out]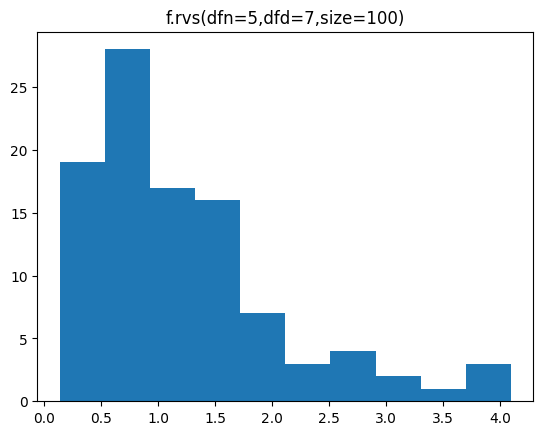

F분포의 확률 밀도 함수

다음은 카이제곱분포를 따르는 두 개의 분포의 자유도가 (1,1), (2,1), (5,1)일 때 확률 밀도 함수를 도식화한 코드입니다. 여기에서는 이를 사용하는 특별한 예는 들지 않겠습니다.

x = np.arange(0,5,0.1)
ls = ['-','-.',':']
for i,(d1,d2) in enumerate([(1,1),(2,1),(5,1)]):
  y = f.pdf(dfn=d1,dfd=d1,x=x)
  plt.plot(x,y,linestyle=ls[i],label=f'dfn={d1},dfd={d2}')
plt.legend()
plt.show()

[out]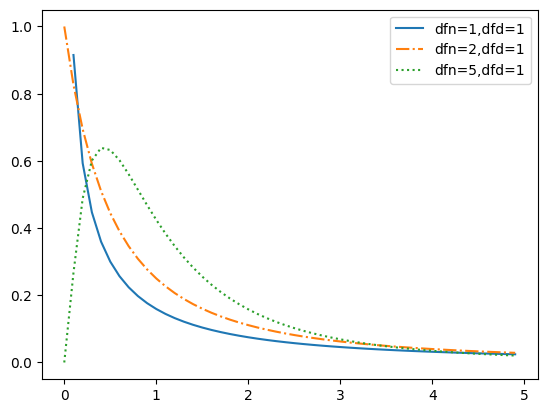

F분포의 누적 분포 함수

f분포의 누적 분포 함수는 cdf입니다.

cdf(x, dfn, dfd, loc=0, scale=1)

앞의 확률 밀도 함수에 대응하는 누적 분포 함수 곡선을 도식해 봅시다.

x = np.arange(0,5,0.1)
ls = ['-','-.',':']
for i,(d1,d2) in enumerate([(1,1),(2,1),(5,1)]):
  y = f.cdf(dfn=d1,dfd=d1,x=x)
  plt.plot(x,y,linestyle=ls[i],label=f'dfn={d1},dfd={d2}')
plt.legend()
plt.title('f.cdf')
plt.show()

[out]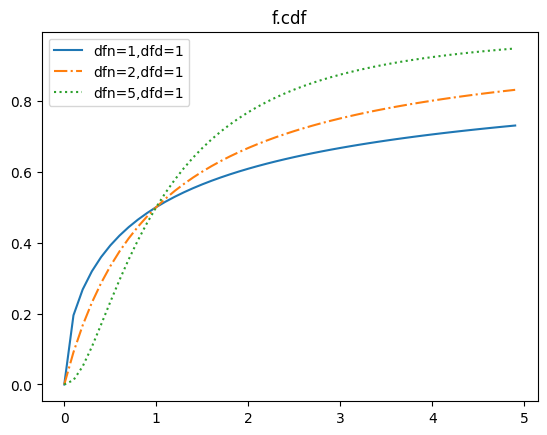

F분포는 두 개의 데이터의 분포가 같은지 비교할 때 사용합니다.

이를 F검정 혹은 등분산성 검정이라고 부릅니다.

등분산성 검정의 F값은 두 개의 데이터의 분산 비율이며 이를 f분포의 1-cdf 혹은 sf함수 결과를 p-value로 사용합니다. (아쉽지만 아직 파이썬에서 F검정 함수는 제공하지 않습니다.

(f_oneway는 단방향 ANOVA 검정으로 등분산성 검정이 아닙니다. )

등분산성 검정을 예를 통해 알아봅시다.

A 학교에서 국어와 영어 과목에 대해 모의 시험을 실시하였다. 다음은 두 과목의 성적 샘플이다.

koean:90,80,75,87,92,80,50,77,68,88,91

english:60, 87, 55, 94,82,40,55,35,92,55,89

먼저 두 개의 샘플의 분산값을 구합니다. (표본이므로 ddof=1로 지정합니다.)

a = np.array([90,80,75,87,92,80,50,77,68,88,91])
b = np.array([60, 87, 55, 94,82,40,55,35,92,55,89])
av = a.var(ddof=1)
bv = b.var(ddof=1)
if av>=bv:
  fv = av/bv
else:
  fv = bv/av
print(fv)

[out]
3.016479663394109

p-value는 1-f.cdf 혹은 f.sf 함수로 구할 수 있습니다.

F분포는 비대칭 분포이며 등분산성 검정은 단측검정 방법으로 수행합니다.

pv = 1 - f.cdf(x=fv,dfn=len(a)-1,dfd=len(b)-1)
print(pv)

[out]
0.048132961921898976

F검정(등분산성 검정)을 수행하는 알고리즘을 함수로 구현하면 다음과 같습니다.

def f_test(s1,s2):
  sv1 = s1.var(ddof=1)
  sv2 = s2.var(ddof=1)

  df1 = len(s1)-1
  df2 = len(s2)-1
  if sv1>= sv2:  
    fv = sv1/sv2
    pv = 1 - f.cdf(x=fv,dfn=df1,dfd=df2)
  else:
    fv = sv2/sv1
    pv = 1 - f.cdf(x=fv,dfn=df1,dfd=df2)
  return fv,pv

앞에 사용한 데이터로 f_test 함수를 사용해 봅시다.

p-value값이 유의 수준보다 크면 귀무 가설을 채택하고 그렇지 않을 때 귀무 가설을 기각합니다.

fv, pv = f_test(a,b)
print(f"f: {fv:.4f} p-value:{pv:.4f}")
if pv>0.05:
  print("귀무 가설을 채택한다. 유의수준 0.05에서 국어와 영어 과목의 분산비는 서로 다르다고 볼 수 없다.")
else:
  print("귀무 가설을 기각한다. 유의수준 0.05에서 국어와 영어 과목의 분산비는 서로 다르다고 볼 수 있다.")

[out]
f: 3.0165 p-value:0.0481
귀무 가설을 기각한다. 유의수준 0.05에서 국어와 영어 과목의 분산비는 서로 다르다고 볼 수 있다.

이를 시각화하면 다음과 같습니다.

코드 설명은 생략하겠습니다.

d1 = len(a)-1
d2 = len(b)-1
x_be = np.linspace(0,fv,20)
x_af = np.linspace(fv,5,20)
y_be = f.pdf(dfn=d1,dfd=d2,x=x_be)
y_af = f.pdf(dfn=d1,dfd=d2,x=x_af)
plt.plot(x_be,y_be,label=f'pdf dfn={d1},dfd={d2} before')
plt.plot(x_af,y_af,label=f'pdf dfn={d1},dfd={d2} afetr')

y2 = f.cdf(dfn=d1,dfd=d2,x=x_be)
plt.plot(x_be,y2,color='r',label=f'cdf dfn={d1},dfd={d2}')

plt.axvline(x=fv,color='k',label=f'fv={fv:.4f}')
y3 = f.pdf(dfn=d1,dfd=d2,x=x_be)
plt.fill_between(x_be,y3,color='g')

plt.text(1,0.2,f'{1-pv:.4f}')
y4 = f.pdf(dfn=d1,dfd=d2,x=x_af)
plt.fill_between(x_af,y4,color='r')
plt.text(fv+0.5,0.2,f'{pv:.4f}')
plt.legend()
plt.show()

[out]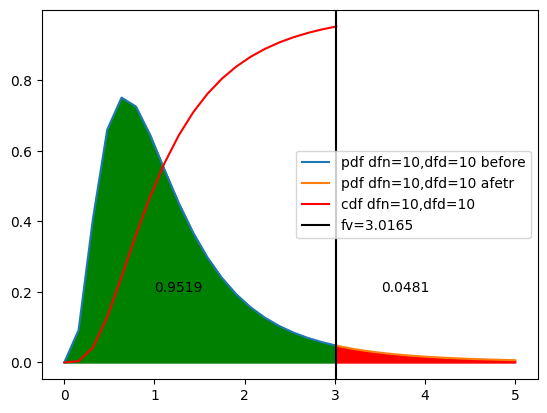

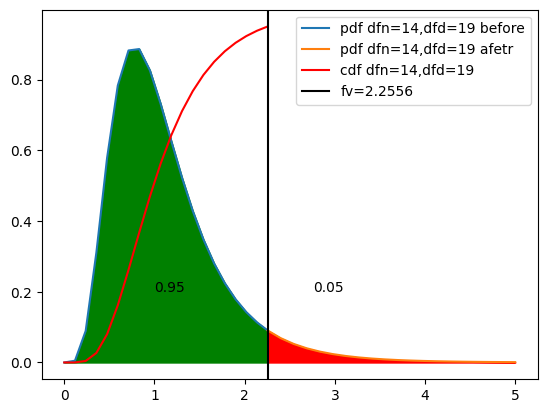
F분포의 퍼센트 포인트 함수

F분포의 퍼센트 포인트 함수는 ppf입니다.

ppf(q, dfn, dfd, loc=0, scale=1)

F검정을 수행할 때 특정 유의 수준에서 귀무 가설을 채택 혹은 기각하는 경계를 구한다고 할 때 ppf를 사용할 수 있습니다.

예를 통해 알아봅시다.

샘플 개수가 15, 20개인 데이터가 있다.

두 개의 데이터의 분포가 같은지 F검정(등분산성 검정)을 수행할 때 유의수준 0.05에서 귀무 가설을 기각 및 채택하는 F값은 얼마인지 구하시오.

n1 = 15
n2 = 20
fv = f.ppf(dfn=n1-1, dfd=n2-1,q=0.95)
print(fv)
f.cdf(dfn=n1-1,dfd=n2-1,x=fv)

이를 도식화해 봅시다.

d1 = n1-1
d2 = n2-1
x_be = np.linspace(0,fv,20)
x_af = np.linspace(fv,5,20)
y_be = f.pdf(dfn=d1,dfd=d2,x=x_be)
y_af = f.pdf(dfn=d1,dfd=d2,x=x_af)
plt.plot(x_be,y_be,label=f'pdf dfn={d1},dfd={d2} before')
plt.plot(x_af,y_af,label=f'pdf dfn={d1},dfd={d2} afetr')

y2 = f.cdf(dfn=d1,dfd=d2,x=x_be)
plt.plot(x_be,y2,color='r',label=f'cdf dfn={d1},dfd={d2}')

plt.axvline(x=fv,color='k',label=f'fv={fv:.4f}')
y3 = f.pdf(dfn=d1,dfd=d2,x=x_be)
plt.fill_between(x_be,y3,color='g')

plt.text(1,0.2,'0.95')
y4 = f.pdf(dfn=d1,dfd=d2,x=x_af)
plt.fill_between(x_af,y4,color='r')
plt.text(fv+0.5,0.2,'0.05')
plt.legend()
plt.show()