다항 회귀(Polynomial Regression) – 머신러닝 with 파이썬

사용할 모듈 포함문

from sklearn.linear_model import LinearRegression #선형 회귀
from sklearn.preprocessing import PolynomialFeatures #다항 특성

from sklearn.model_selection import train_test_split #학습 및 테스트 데이터 분리
from sklearn.metrics import r2_score #r2 결정 계수(회귀)
from sklearn.model_selection import cross_val_score #교차 검증 점수

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

다항 회귀 (Polynomial Regression)

선형 회귀 모델은 학습을 통해 선형 회귀 함수를 도출합니다.

하지만 독립 변수와 종속 변수의 관계를 다항 관계로 표현하는 것이 더 좋을 수 있습니다. 2차 방정식 이상의 관계를 갖을 수 있다는 것이죠.

이 때 독립 변수의 특성을 다항 특성으로 변환하면 선형 모델로도 다항 관계를 도출할 수 있습니다.

파이썬 사이킷 런에서는 PolynomialFeatures를 통해 다항 특성으로 변환을 지원하고 있습니다.

class sklearn.preprocessing.PolynomialFeatures(degree=2, *, interaction_only=False, include_bias=True, order=’C’)

PolynomialFeatures 메뉴얼 사이트

예를 들어 2 개의 특성을 갖는 2개의 독립 변수를 2차 방정식에 맞게 특성 변환을 해 봅시다.

data = [[1,2],[3,4]]
pf = PolynomialFeatures(degree=2)
data_p2 = pf.fit_transform(data)
print(data_p2)
[out]
[[ 1.  1.  2.  1.  2.  4.]
 [ 1.  3.  4.  9. 12. 16.]]

결과를 보면 [a,b]의 특성이 [1, a, b, aa, ab,bb]로 변환해 주는 것을 알 수 있습니다.

bias 부분은 언제나 1로 변환해서 생략해서 변환하는 것이 일반적입니다.

다음은 bias 부분을 생략하여 특성 변환하는 예입니다.

pf = PolynomialFeatures(degree=2,include_bias=False)
data_p2 = pf.fit_transform(data)
print(data_p2)
[out]
[[ 1.  2.  1.  2.  4.]
 [ 3.  4.  9. 12. 16.]]

실험에 사용할 데이터

다음은 여러 용기의 높이와 부피 데이터들입니다.

heights = np.array([8,20,28,42,53,63,73,78,90,102,108,122,128,138,153,162,167,173,176,177,181])
volumns = np.array([1,2,5,9,15,19,27,32,39,55,60,77,89,108,123,138,153,170,190,218,230])

이를 시각화해서 보면 다음과 같습니다.

plt.figure(figsize=(4,4))
plt.plot(heights,volumns,'.')
plt.xlim(0,240)
plt.ylim(0,240)
plt.xlabel('height')
plt.ylabel('volumn')
plt.show()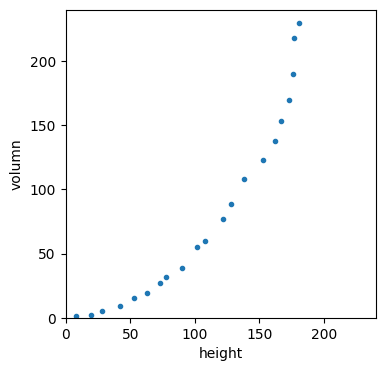
높이와 부피 관계 시각화
높이와 부피 관계 시각화
  • 원래 값 그대로 선형 모델로 학습

먼저 특성을 변환하지 않고 선형 모델로 학습시켜 봅시다.

사이킷 런에서 학습할 독립 변수는 (sample 수, 독립변수 수) 구조의 2차원이어야 합니다.

이에 맞게 구조 변경할게요.

x = heights.reshape(-1,1)
y = volumns

선형 모델을 생성하고 학습할게요.

그리고 높이 구간 0~240으로 부피를 예측해 봅시다.

model = LinearRegression()
model.fit(x,y)
boudary = [[0],[240]]
pred = model.predict(boudary)
print(f'{boudary} : {pred}')
print(f'y = {model.coef_[0]:.2f}*x{model.intercept_:+.2f}')
[out]
[[0], [240]] : [-48.21291782 248.57258879]
y = 1.24*x-48.21

이를 시각화 합시다.

plt.figure(figsize=(4,4))
plt.plot(heights,volumns,'.')
plt.plot([0,240],pred,label=f'{model.coef_[0]:.2f}*x{model.intercept_:+.2f}')
plt.xlim(0,240)
plt.ylim(0,240)
plt.xlabel('height')
plt.ylabel('volumn')
plt.legend()
plt.show()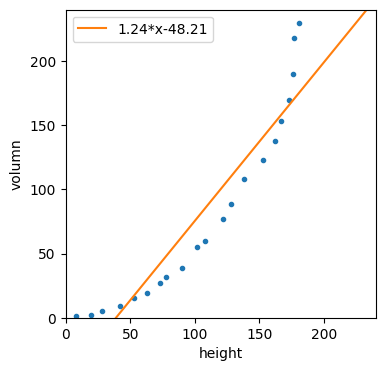
높이와 부피의 선형 회귀 결과
높이와 부피의 선형 회귀 결과

보시는 것처럼 실제 데이터는 곡선의 형태에 가까운데 선형 회귀 결고는 직선의 형태를 지니고 있습니다.

이럴 때 특성을 다항 특성으로 변환하면 더 나은 예측을 할 수 있습니다.

  • 다항 특성으로 변환 후 선형 모델로 학습

먼저 2차 방정식에 맞게 다항 특성으로 변환합시다.

pf = PolynomialFeatures(degree=2,include_bias=False)
pf_x = pf.fit_transform(x)
print(f'원본 구조:{x.shape} 변환 후 구조:{pf_x.shape}')
[out]
원본 구조:(21, 1) 변환 후 구조:(21, 2)

2차 방정식에 맞게 특성 변환하여 구조가 바뀐 것을 알 수 있습니다. 

print(x[0], pf_x[0])
[out]
[8] [ 8. 64.]

결과를 보면 알 수 있듯이 [a] 특성이 [a,aa] 형태로 변환한 것입니다.

선형 모델로 다시 학습해 봅시다.

model = LinearRegression()
model.fit(pf_x,y)
w1 = model.coef_[0]
w2 = model.coef_[1]
b = model.intercept_
print(f"회귀식: y = {w2:.2f}*x^2 {w1:+.2f}*x {b:+.2f} ")
[out]
회귀식: y = 0.01*x^2 -0.47*x +11.50

선형 모델이지만 특성 자체를 다항 특성으로 변환하였기 때문에 2차 방정식에 해당하는 다항 회귀식을 도출할 수 있습니다.

구간 [0,240]에 있는 값을 5 간격으로 예측해 시각화 해 봅시다.

sx = np.array(range(0,240,5)).reshape(-1,1)
pf_sx = pf.fit_transform(sx)
pred = model.predict(pf_sx)
plt.figure(figsize=(4,4))
plt.plot(heights,volumns,'b.',label='actual')
plt.plot(sx,pred,'r',label='regression function line')
plt.xlim(0,240)
plt.ylim(0,240)
plt.xlabel('height')
plt.ylabel('volumn')
plt.legend()
plt.title(f"y = {w2:.2f}*x^2 {w1:+.2f}*x {b:+.2f} ")
plt.show()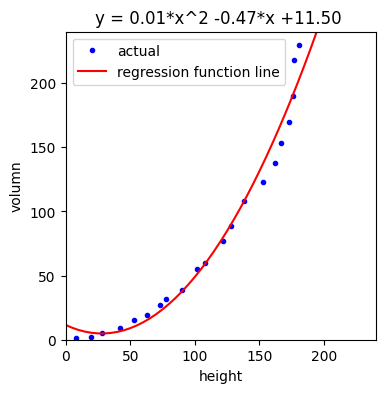
높이_부피 2차 방정식으로 특성 변환 후 선형 회귀
높이_부피 2차 방정식으로 특성 변환 후 선형 회귀

차원을 높일 수록 학습 데이터에 민감하게 학습하는 경향을 보입니다.

다음은 10차 방정식에 맞게 특성 변환한 코드입니다.

pf = PolynomialFeatures(degree=10,include_bias=False)
pf_x10 = pf.fit_transform(x)
print(pf_x10.shape)
[out]
(21, 10)

선형 모델로 학습 후 시각화 합시다.

model = LinearRegression()
model.fit(pf_x10,y)
pred = model.predict(pf_x10)
plt.figure(figsize=(4,4))
plt.plot(heights,volumns,'b.',label='actual')
plt.plot(heights,pred,'r',label='predict')
plt.xlim(0,240)
plt.ylim(0,240)
plt.xlabel('height')
plt.ylabel('volumn')
plt.legend()
plt.show()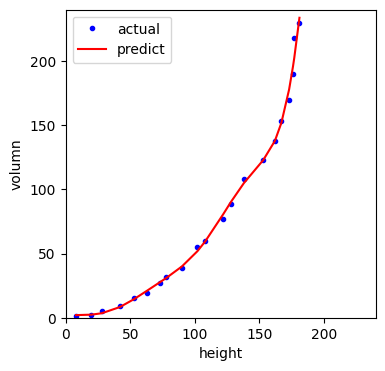
높이_부피 10차 방정식으로 특성 변환 후 선형 회귀
높이, 부피 10차 방정식으로 특성 변환 후 선형 회귀

보시는 것처럼 학습한 데이터에 매우 민감하게 학습한 것을 알 수 있습니다.

하지만 학습에 사용하지 않은 다른 데이터에도 적합한 지 알 수 없습니다.

학습 데이터에서는 매우 정확한 결과를 예측하여 모델 적합도에 높은 점수를 주었다고 가정합시다.

만약 실제 데이터에서 매우 나쁜 결과를 예측한다면 이는 매우 큰 낭패겠죠.

이러한 현상을 과적합(overfitting, 오버 피팅)이라고 말합니다.

선형 모델에서 과적합 문제를 해결하기 위한 방법으로 규제(라쏘, 리지, 엘라스틱 넷)를 제공합니다. 이에 관해서는 다음에 알아보기로 합시다.

학생 건강 데이터

이번에는 학생의 키로 몸무게를 예측하는 것을 해 봅시다.

데이터는 공공 데이터 포털에서 2015년 학생 신체 검사 데이터를 얻어온 후 필요한 항목만 편집한 것입니다.

df = pd.read_csv('https://raw.githubusercontent.com/ehpub/ML-with-Python/main/stu_health_2015.csv')
df.info()
[out]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 9686 entries, 0 to 9685
Data columns (total 2 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   height  9686 non-null   float64
 1   weight  9682 non-null   float64
dtypes: float64(2)
memory usage: 151.5 KB

결측 치를 제거한 후 키와 몸무게를 독립 변수와 종속 변수로 선택합시다.

DataFrame에서 독립 변수는 슬라이스로 선택하고 종속 변수는 해당 컬럼을 인덱서를 선택합니다.

df = df.dropna(axis=0)
data = df[['height']]
target = df['weight']

학습 데이터, 검증 데이터, 테스트 데이터로 분리시킵시다.

x_train, x_test, y_train, y_test = train_test_split(data,target)
x_train2,x_val, y_train2,y_val = train_test_split(x_train,y_train)
print(y_train2.shape, y_val.shape, y_test.shape)
[out]
(5445,) (1816,) (2421,)
  • 학습, 검증 후 평가

먼저 다항 회귀를 적용하지 않고 모델 학습 및 검증을 시행합시다.

print("다항 회귀 적용 X 모델 학습 및 검증")
model = LinearRegression()
model.fit(x_train2,y_train2)
pred_val = model.predict(x_val)
print(f"R2 결정 계수:{r2_score(y_val,pred_val):.4f}")
[out]
다항 회귀 적용 X 모델 학습 및 검증
R2 결정 계수:0.7238

R2 결정 계수가 0.7238이 나왔네요. 이 정도면 학습 결과가 나쁘지 않네요.

이번에는 다항 회귀를 적용한 후 모델 학습 및 검증해 봅시다.

print("다항 회귀 적용 O 모델 학습 및 검증")
for d in range(2,5):
  pf = PolynomialFeatures(degree=d,include_bias=False)
  pf.fit(x_train2)
  x_train_p =pf.transform(x_train2)
  model = LinearRegression()
  print("###degree",d)
  model.fit(x_train_p,y_train2)
  x_val_p = pf.transform(x_val)
  pred_val = model.predict(x_val_p)
  print(f"R2 결정 계수:{r2_score(y_val,pred_val):.4f}")
[out]
다항 회귀 적용 O 모델 학습 및 검증
###degree 2
R2 결정 계수:0.7273
###degree 3
R2 결정 계수:0.7284
###degree 4
R2 결정 계수:0.7284

R2 결정 계수가 모두 비슷하네요.

그 중에 제일 높은 3차 방정식에 맞게 특성 변환 후 모델을 평가해 봅시다. 

print("모델 평가")
pf = PolynomialFeatures(degree=3,include_bias=False)
pf.fit(x_train)
x_train_p =pf.transform(x_train)
x_test_p = pf.transform(x_test)

model = LinearRegression()
print("###degree",3)
model.fit(x_train_p,y_train)

pred_test = model.predict(x_test_p)
print(f"R2 결정 계수:{r2_score(y_test,pred_test):.4f}")
[out]
모델 평가
###degree 3
R2 결정 계수:0.7300

테스트 데이터에도 비슷한 수준의 R2 결정 계수가 나왔네요.

이처럼 학습 데이터 점수와 테스트 점수가 비슷하게 나오면 과적합(overfitting)은 아닌 것으로 판단할 수 있씁니다.

  • 교차 검증 후 평가

이번에는 교차 검증을 통해 같은 실험을 해 볼게요.

먼저 특성 변환하기 전에 교차 검증 및 평가입니다.

print("다항 회귀 적용 X 모델 학습 및 검증")
model = LinearRegression()
scores = cross_val_score(model,x_train,y_train)
print(f"교차 검증 점수(평균):{scores.mean():.4f}")
model.fit(x_train,y_train)
pred_test = model.predict(x_test)
print(f"R2 결정 계수:{r2_score(y_test,pred_test):.4f}")
[out]
다항 회귀 적용 X 모델 학습 및 검증
교차 검증 점수(평균):0.7184
R2 결정 계수:0.7269

교차 검증 점수도 비슷하게 나오네요.

이번에는 다항 회귀를 적용해 봅시다.

print("다항 회귀 적용 O 모델 학습 및 검증")
for d in range(2,5):
  pf = PolynomialFeatures(degree=d,include_bias=False)
  pf.fit(x_train)
  x_train_p =pf.transform(x_train)
  x_test_p =pf.transform(x_test)
  model = LinearRegression()
  print("###degree",d)
  scores = cross_val_score(model,x_train_p,y_train)
  print(f"교차 검증 점수(평균):{scores.mean():.4f}")
  model.fit(x_train_p,y_train)
  pred_test = model.predict(x_test_p)
  print(f"R2 결정 계수:{r2_score(y_test,pred_test):.4f}")
[out]
다항 회귀 적용 O 모델 학습 및 검증
###degree 2
교차 검증 점수(평균):0.7222
R2 결정 계수:0.7297
###degree 3
교차 검증 점수(평균):0.7229
R2 결정 계수:0.7300
###degree 4
교차 검증 점수(평균):0.7229
R2 결정 계수:0.7300

모두 점수가 비슷하네요.

이번 실험에서는 선형 모델로 나쁘지 않게 예측할 수 있음을 알 수 있고 다항 회귀를 여부에 큰 상관없음도 확인하였습니다.

다음은 다항 회귀를 적용하기 전 데이터와 예측 값을 시각화 한 것입니다.

예측 값은 직선(선형 회귀 함수) 위에 있음을 알 수 있습니다.

model = LinearRegression()
print("###degree",1)
model.fit(data,target)
pred_val = model.predict(data)
plt.figure(figsize=(4,4))
plt.plot(data,target,'b.',label='actual')
plt.plot(data,pred_val,'r.',label='predict')
plt.xlabel('height')
plt.ylabel('weight')
plt.legend()
plt.title('degree=1')
plt.show()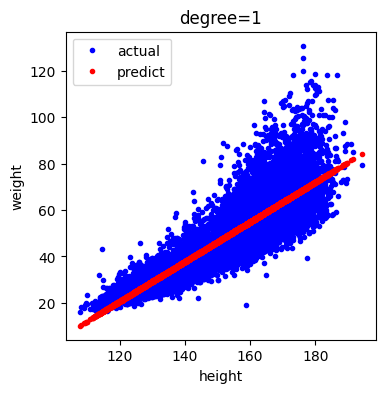
키와 몸무게 선형 회귀
키와 몸무게 선형 회귀

다음은 특성 변환하였을 때 데이터와 예측 값을 시각화한 것입니다.

for d in range(2,5):
  pf = PolynomialFeatures(degree=d,include_bias=False)
  pf.fit(data)
  data_p =pf.transform(data)
  model = LinearRegression()
  print("###degree",d)
  model.fit(data_p,target)
  pred_val = model.predict(data_p)
  plt.figure(figsize=(4,4))
  plt.plot(data,target,'b.',label='actual')
  plt.plot(data,pred_val,'r.',label='predict')
  plt.xlabel('height')
  plt.ylabel('weight')
  plt.legend()
  plt.title(f'degree={d}')
  plt.show()
[out]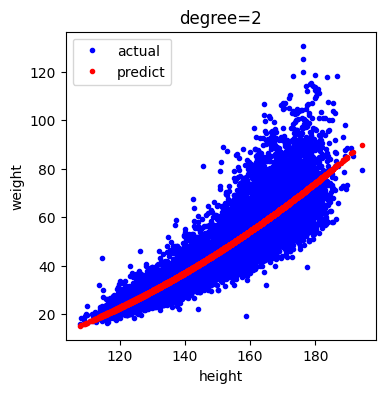
키와 몸무게 2차 방적식으로 특성 변환 후 선형 회귀
키와 몸무게 2차 방적식으로 특성 변환 후 선형 회귀
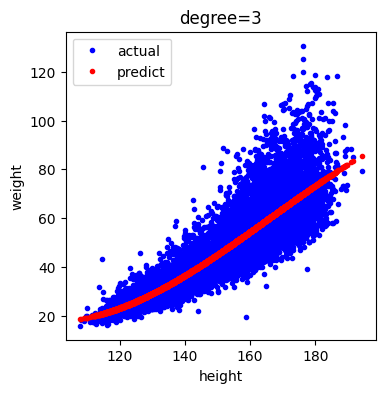
키와 몸무게 3차 방적식으로 특성 변환 후 선형 회귀
키와 몸무게 3차 방적식으로 특성 변환 후 선형 회귀
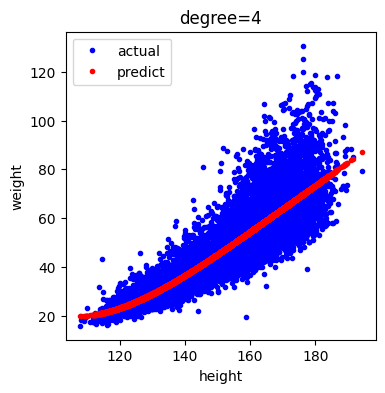
키와 몸무게 4차 방적식으로 특성 변환 후 선형 회귀
키와 몸무게 4차 방적식으로 특성 변환 후 선형 회귀

특성 변환 후 결과를 시각화 한 것을 보면 약간의 휘어짐은 있지만 직선에 가까운 곡선 형태임을 알 수 있습니다.

지하철 대기 데이터 초미세먼지 예측하기

이번에는 공공데이터 포털에서 2022에 배포한 지하철 대기 데이터를 이용하여 초미세먼지를 예측해 봅시다.

path = 'https://raw.githubusercontent.com/ehpub/ML-with-Python/main/subway_air_2022.csv'
df = pd.read_csv(path,encoding='cp949')
df.info()
[out]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 263 entries, 0 to 262
Data columns (total 9 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   연번       263 non-null    int64  
 1   호선       263 non-null    object 
 2   역명       263 non-null    object 
 3   미세먼지     263 non-null    float64
 4   초미세먼지    263 non-null    float64
 5   이산화탄소    263 non-null    int64  
 6   폼알데하이드   263 non-null    float64
 7   일산화탄소    263 non-null    float64
 8   데이터기준일자  263 non-null    object 
dtypes: float64(4), int64(2), object(3)
memory usage: 18.6+ KB

미세먼지, 일산화탄소, 폼알데하이드, 이산화탄소 특성으로 초미세먼지를 예측해 봅시다.

이번 실험은 과적합을 확인하기 위해서입니다.

여기에서는 시각화 결과를 인지하기 쉽게 하기 위해 50개의 데이터만 가지고 실험할게요. 

data = df[['미세먼지','일산화탄소','폼알데하이드','이산화탄소']].values[:50]
target = df['초미세먼지'][:50].values
x_train, x_test, y_train, y_test = train_test_split(data,target)
x_train2,x_val, y_train2,y_val = train_test_split(x_train,y_train)
print(y_train2.shape, y_val.shape, y_test.shape)
[out]
(27,) (10,) (13,)

먼저 다항 회귀를 적용하기 전의 데이터로 학습 및 검증합시다.

print("다항 회귀 적용 X 모델 학습 및 검증")
model = LinearRegression()
model.fit(x_train2,y_train2)
pred_val = model.predict(x_val)
print(f"R2 결정 계수:{r2_score(y_val,pred_val):.4f}")
[out]
다항 회귀 적용 X 모델 학습 및 검증
R2 결정 계수:0.6888

R2 결정 계수가 0.6888로 나쁘지 않네요.

다음은 특성 변환 후에 학습 및 검증해 봅시다.

print("다항 회귀 적용 O 모델 학습 및 검증")
for d in range(2,5):
  pf = PolynomialFeatures(degree=d,include_bias=False)
  pf.fit(x_train2)
  x_train_p =pf.transform(x_train2)
  model = LinearRegression()
  print("###degree",d)
  model.fit(x_train_p,y_train2)
  x_val_p = pf.transform(x_val)
  pred_val = model.predict(x_val_p)
  print(f"R2 결정 계수:{r2_score(y_val,pred_val):.4f}")
[out]
다항 회귀 적용 O 모델 학습 및 검증
###degree 2
R2 결정 계수:-0.1329
###degree 3
R2 결정 계수:-166.5900
###degree 4
R2 결정 계수:-2492.3391

변환 차수가 높을 수로 R2 결정 계수가 극악해 지네요.

실험 결과를 직관적으로 확인할 수 있게 시각화 합시다.

먼저 특성 변환 전입니다.

model = LinearRegression()
model.fit(x_train,y_train)
pred_train = model.predict(x_train)
pred_test = model.predict(x_test)

fig,axs = plt.subplots(ncols=2,figsize=(8,4))
axs[0].plot(y_train,'bo',label='actual')
axs[0].plot(pred_train,'r.',label='predict')
axs[0].set_title('train')
axs[1].plot(y_test,'bo',label='actual')
axs[1].plot(pred_test,'r.',label='predict')
axs[1].set_title('test')
plt.suptitle(f'degree=1')
plt.legend()
plt.show()
diff = pred_test - y_test
print("최대 오차:",np.abs(diff).max())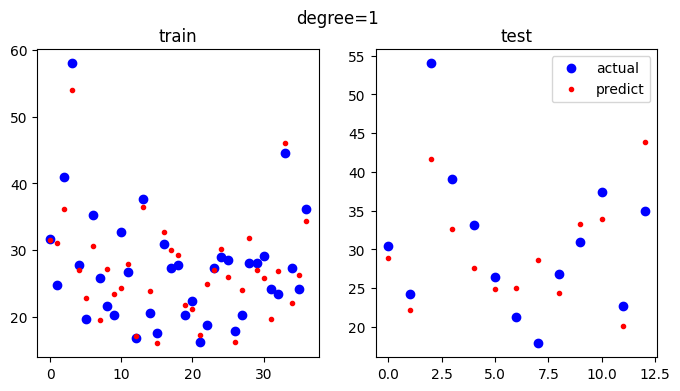
특성 변환 하기 전 초미세먼지 선형 회귀
특성 변환 하기 전 초미세먼지 선형 회귀
[out]
최대 오차: 12.326388594083994

오른쪽 도면이 테스트 데이터와 예측 값인데 최대 오차가 12.32 정도 나왔네요.

이번에는 특성 변환 후에 시각화 합시다.

for d in range(2,5):
  pf = PolynomialFeatures(degree=d,include_bias=False)
  pf.fit(x_train)
  x_train_p =pf.transform(x_train)
  x_test_p =pf.transform(x_test)

  model = LinearRegression()
  print("###degree",d)
  model.fit(x_train_p,y_train)
  pred_train = model.predict(x_train_p)
  pred_test = model.predict(x_test_p)
  
  fig,axs = plt.subplots(ncols=2,figsize=(8,4))
  axs[0].plot(y_train,'bo',label='actual')
  axs[0].plot(pred_train,'r.',label='predict')
  axs[0].set_title('train')
  
  axs[1].plot(y_test,'bo',label='actual')
  axs[1].plot(pred_test,'r.',label='predict')
  axs[1].set_title('test')

  plt.suptitle(f'degree={d}')
  plt.legend()
  plt.show()
  diff = pred_test - y_test
  print("최대 오차:",np.abs(diff).max())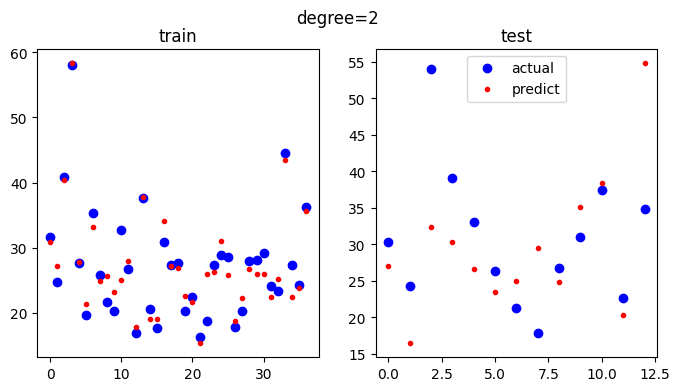
2차 방정식으로 특성 변환 후 초미세먼지 선형 회귀
2차 방정식으로 특성 변환 후 초미세먼지 선형 회귀
[out]
최대 오차: 21.63646810856676

2차 방정식으로 변환하였을 때의 최대 오차는 21.63이네요.

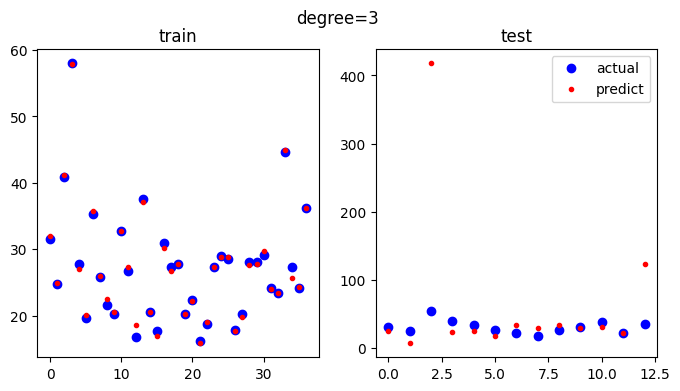
3차 방정식으로 특성 변환 후 초미세먼지 선형 회귀
3차 방정식으로 특성 변환 후 초미세먼지 선형 회귀

3차 방정식으로 변환하였을 때의 학습 데이터 부분은 매우 정확해 졌네요.

[out]
최대 오차: 363.774002753632

하지만 테스트 데이터는 최대 오차가 363이 넘네요. y축의 범위를 보면 테스트 데이터의 실제 값은 10~60 사이인데 예측 값은 0~420 사이입니다. 이 정도면 과적합이 뚜렷하다고 볼 수 있어요.

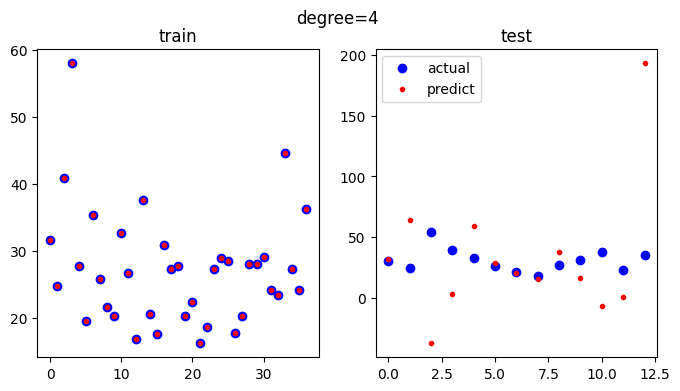
4차 방정식으로 특성 변환 후 초미세먼지 선형 회귀
4차 방정식으로 특성 변환 후 초미세먼지 선형 회귀
[out]
최대 오차: 158.19396346647622

4차 방정식으로 특성 변환하였을 때를 보십시오.

학습 데이터 부분을 보면 예측 값이 거의 일치하는 것을 알 수 있어요.

하지만 테스트 부분을 보면 오차가 큰 것을 알 수 있습니다.

여러분은 독립 변수로 어떠한 특성을 어떻게 변환하였을 때 좋은 결과를 얻을 수 있는지 다양한 실험을 수행할 수 있고 결과를 판단할 수 있어야 합니다.

머신러닝 with 파이썬