t 분포

사용할 모듈 포함문

import scipy as sp
from scipy import stats
from scipy.stats import t
from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

t 분포는 모집단의 표준편차를 구하기 어려울 때 표본의 표준편차를 사용하여 표준화를 시도하는 분포를 말합니다.

유튜브 동영상 강의로 보기

위키백과 – 스튜던트 t분포

t분포 평균과 표준편차 구하기

예를 통해 t분포의 평균과 표준편차를 구해봅시다.

다음은 A학교 10명의 학생 키이다.(단위는 cm)

173,180,179,165,172,167,175,177,172,180

모집단의 평균 키와 표준편차를 예측하시오.

평균은 기댓값이 모수와 같은 불편추정량이라 일반적인 평균 계산으로 추정할 수 있습니다.

표준편차는 불편추정량이 아닙니다. 표본으로 표준편차를 구할 때는 자료 개수 n이 아닌 자유도(n-1)로 나누어서 구합니다.

위키백과 – 불편 추정량

data = np.array([173,180,179,165,172,167,175,177,172,180])
print("평균:",data.mean())
print("표준편차:",data.std(ddof=1))

[out]
평균: 174.0
표준편차: 5.228129047119374

참고로 자유도를 고려하지 않았을 때 표본 편차는 다음과 같습니다.

data.std() #자유도를 적용하지 않았을 때

[out]
4.959838707054898

t 분포를 따르는 샘플 생성하기

t 분포의 샘플을 생성하는 함수도 rvs 입니다.

t 분포에서는 자유도를 df 인자로 전달해 주어야 합니다.

다음은 평균 174, 표준편차 7이며 자유도가 99인 샘플 10개를 생성하는 코드입니다.

(표본 100개의 평균이 174, 표준편차가 7일 때 이를 이용하여 10개의 샘플을 구하는 것입니다. 실제는 표본보다 많은 개숭의 샘플을 구할 때가 많습니다.)

height_t_sample =  t.rvs(size=10,loc=174,scale=7,df=99)
print(height_t_sample)

[out]
[179.42431315 168.03551913 181.73255413 171.7837546  174.17083326
 168.86622021 177.07276136 184.30734496 158.77872558 174.50717195]

t 분포 샘플과 정규분포 샘플을 생성하여 비교하기

t 분포로 샘플을 생성(t.rvs)하는 것과 정규분포로 샘플을 생성(norm.rvs)하였을 때 차이를 비교해 봅시다. 단순히 생성한 샘플 값을 확인하는 것으로는 비교가 어렵습니다.

여기에서는 자유도 2, 3, 5, 100일 때 같은 조건(평균: 174, 표준편차:7)으로 1000회 실험하였을 때 나오는 데이터의 분포를 비교하여 시각화하기로 할게요.

bins=range(130,220)
for n in [2,3,5,100]:
  ts = []
  ns = []
  for _ in range(1000):
    t_sample =  t.rvs(size=n,loc=174,scale=7,df=n-1)
    ts.extend(t_sample.tolist())
    n_sample =  norm.rvs(size=n,loc=174,scale=7)
    ns.extend(n_sample.tolist())
  plt.hist(ts,bins=bins,alpha=0.7,edgecolor='r',label='t')
  plt.hist(ns,bins=bins,alpha=0.7,edgecolor='b',label='normal')
  plt.legend()
  plt.title(f'n={n}')
  plt.show()

[out]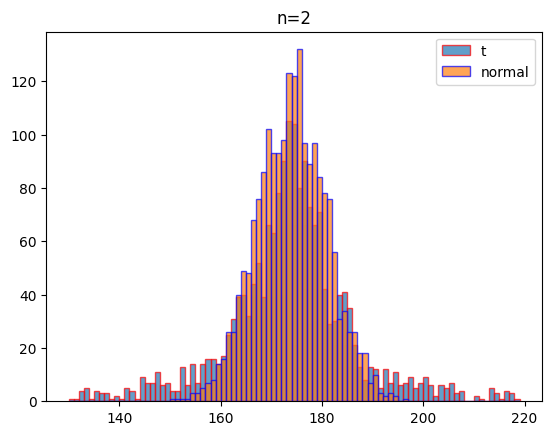

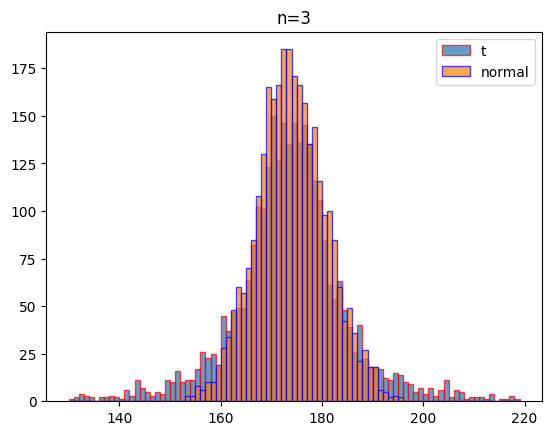
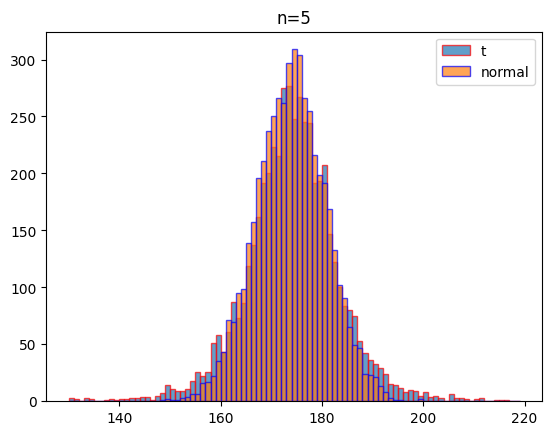
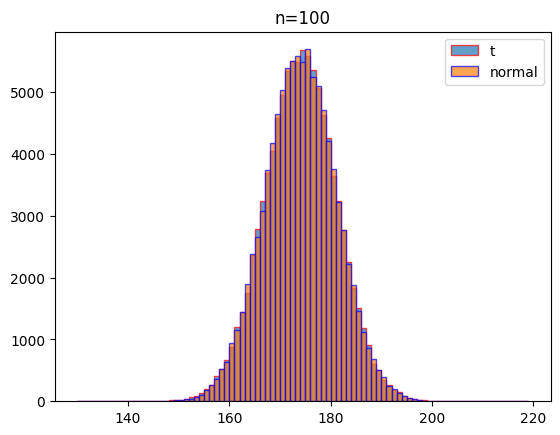
시각화 결과를 보는 것처럼 자유도가 커질 수도 t분포는 정규분포에 가까워 짐을 알 수 있습니다.

t 확률 밀도 함수와 정규분포 확률 밀도 함수 도식화

이번에는 확률 밀도 함수로 t분포와 정규 분포를 시각화해 볼게요.

bins=range(130,220)
for n in [2,3,5,100]:
  ny = norm.pdf(bins,loc=174,scale=7)
  ty = t.pdf(bins,loc=174,scale=7,df=n-1)
  plt.plot(ny,label='norm')
  plt.plot(ty,':',label='t')
  plt.legend()
  plt.title(f'n={n}')
  plt.show()

[out]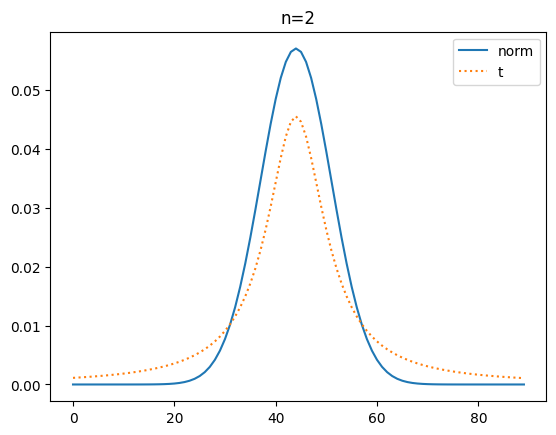

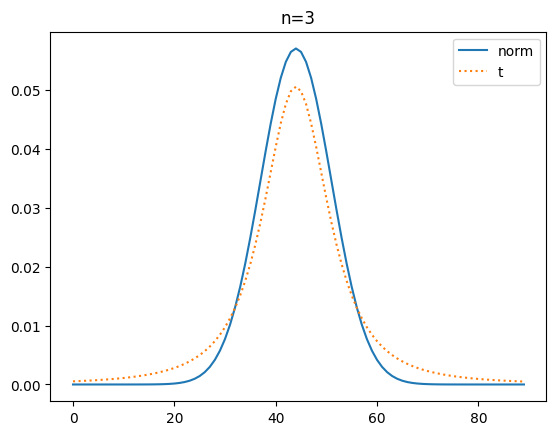
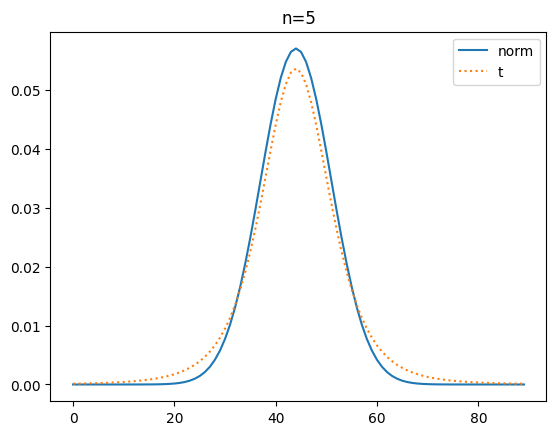
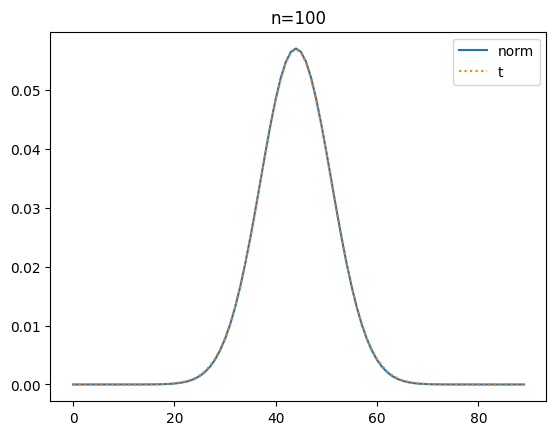
확률 밀도 함수(pdf)로 비교해 보니 자유도가 커질 수도 t분포가 정규분포에 가까워 짐을 명확히 알 수가 있네요.

t 분포에서 확률 관련 함수 사용하기

이번에는 대략적으로 t분포를 이용하여 확률을 예측하는 것을 해 봅시다.

ㄱ시에 있는 8월에 온도를 계측한 결과 중 10개는 다음과 같습니다. (단위는 섭씨)

23, 30,18, 33, 28, 33, 34, 38, 29, 31

측정 온도가 25일 때 상위 몇%에 속할지 예측하시오.

data = np.array([23, 30,18, 33, 28, 33, 34, 38, 29, 31])
d_mean = data.mean()
d_std = data.std(ddof=1)
print("평균:",d_mean)
print("표준편차:",d_std)

[out]
평균: 29.7
표준편차: 5.735852159879995

자유도를 적용하지 않았을 때 표준편차는 다음과 같습니다.

print("자유도를 적용하지 않았을 때 표준편차:",data.std())

[out]
자유도를 적용하지 않았을 때 표준편차: 5.441507144165117

섭씨 25도일 때 상위 몇 %로 속하는 온도일 때 예측하시오.

(cdf 함수 혹은 sf 함수를 이용하여 예측할 수 있습니다.)

df = len(data)-1
score = 25
p = t.cdf(x=score,loc=d_mean,scale=d_std,df=df)
print(f"{score}는 상위 {(1-p)*100:.2f}%로 예측한다.")
p2 = t.sf(x=score,loc=d_mean,scale=d_std,df=df)
print(f"{score}는 상위 {p2*100:.2f}%로 예측한다.")

[out]
25는 상위 78.31%로 예측한다.
25는 상위 78.31%로 예측한다.

25점에서 35도 사이일 확률을 예측하시오.

low = 25
high = 35
lp = t.cdf(q=low,loc=d_mean,scale=d_std,df=df)
hp = t.cdf(x=high,loc=d_mean,scale=d_std,df=df)
print(f"[{low},{high}] 구간에 속할 확률은 {(hp-lp)*100:.2f}%로 예측한다.")

[out]
[25,35] 구간에 속할 확률은 59.33%로 예측한다.

상위 5%에 속하는 온도의 기준은 얼마 이상인지 예측하시오.

p = 1-0.05
temp = t.ppf(q=p,loc=d_mean,scale=d_std,df=df)
print(f"상위 {p*100}%에 속하는 온도의 기준은 {temp:.2f}이다.")

[out]
상위 95.0%에 속하는 온도의 기준은 40.21이다.