중심 극한 정리 – 파이썬으로 다루는 통계

정규분포를 다루면서 독립적인 확률 변수들의 평균은 중심 극한 정리를 따른다고 하였습니다.

이번에는 이를 증명해 보기로 할게요.

동영상 강의는 언제나 휴일 유튜브에 게시하였습니다.

다음은 실험에 사용할 모듈 포함문입니다.

import scipy as sp
from scipy import stats
from scipy.stats import norm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

중심 극한 정리

같은 확률 분포(균등 분포 확률)를 갖는 독립 확률 변수의 분포는 n(확률 변수의 개수)이 충분히 크면 정규 분포에 가까워 진다는 것이 중심 극한 정리입니다.

균등 분포 확률의 확률 밀도 함수 만들기

주사위를 던지는 것처럼 어떤 사건이 발생하는 확률이 같은 균등 분포의 밀도 함수를 구해봅시다.

주사위를 던져서 특정 면(1,2,3,4,5,6)이 나올 확률은 1/6입니다.

주사위를 던져서 나올 수 있는 최댓값 6, 최솟값 1 이며 i면이 나올 확률은 P(i) = 1/((6+1)-1)입니다.

P(i) = 1/((max-1)-min)

이를 함수로 구현하면 다음처럼 구현할 수 있습니다.

def uniform_pdf(x,min_v, max_v):
  max_p1 = max_v+1
  if min_v<= x < max_p1:
    return 1/(max_p1 - min_v)
  return 0

uniform_pdf 함수를 사용하는 예입니다.

for i in range(-3,10):
  print(f"P({i}) = {uniform_pdf(i,1,6)}")

[out]
P(-3) = 0
P(-2) = 0
P(-1) = 0
P(0) = 0
P(1) = 0.16666666666666666
P(2) = 0.16666666666666666
P(3) = 0.16666666666666666
P(4) = 0.16666666666666666
P(5) = 0.16666666666666666
P(6) = 0.16666666666666666
P(7) = 0
P(8) = 0
P(9) = 0

이를 시각화 해 볼게요.

dice_sides = range(-3,10)
dss = [str(i) for i in dice_sides] 
px = [uniform_pdf(i,1,6) for i in dice_sides]
plt.bar(dss,px)
plt.xlabel('dice side')
plt.ylabel('P(dice side)')
plt.ylim(0,1)
plt.title('draw dice')
plt.show()

[out]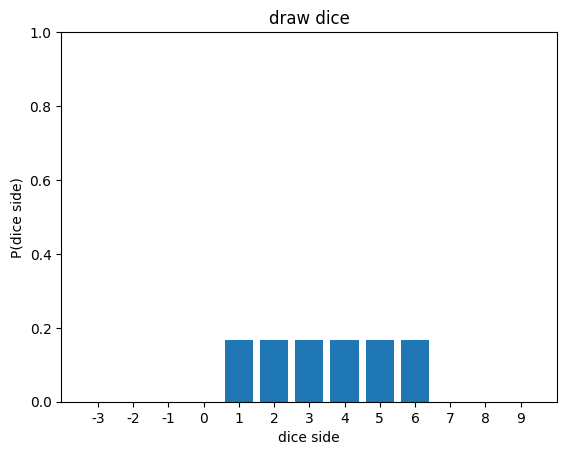

주사위 던지기 실험

베르누이 시행은 실험 결과가 성공 혹은 실패 중에 하나인 실험을 말합니다. 중심 극한 정리를 표현하기 위해 이 함수를 먼저 정의하기로 할게요.

def bernouli_trial(p):
  return 1 if np.random.random()<p else 0

주사위 를 던져서 원하는 면이 나오는지 실험하여 나온 횟수를 반환하는 함수도 만들어 볼게요.

def draw_dice(n=1000,side=1):
  p = uniform_pdf(side,1,6)
  cnt = 0
  for _ in range(n): 
    re = bernouli_trial(p)
    if re == 1:
      cnt+=1
  return cnt

draw_dice 함수에서 n은 주사위를 던지는 횟수이며 side는 나오길 기대하는 면입니다.

draw_dice함수를 인자없이 호출하면 n의 디폴트 값은 1000이므로 주사위를 1000번 던져서 1인 면이 나오는 횟수를 구할 수 있습니다.

이를 10번 수행해 봅시다.

for _ in range(10):
  print(draw_dice())

[out]
172
164
168
147
160
174
165
153
159
160

실험 횟수에 따른 분포 비교하기

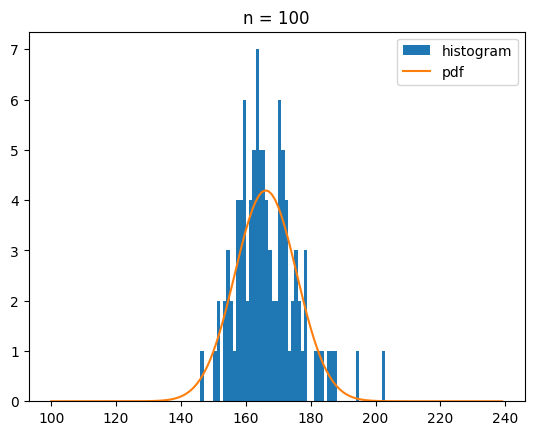
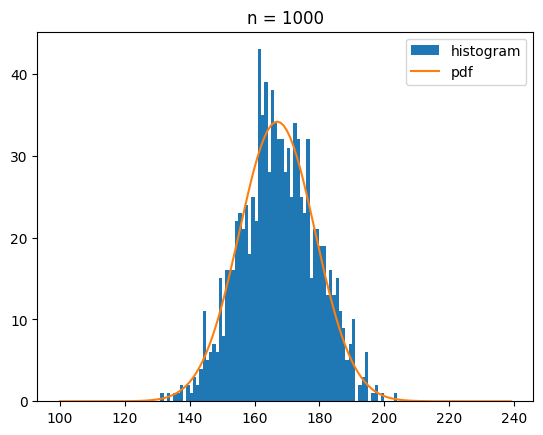
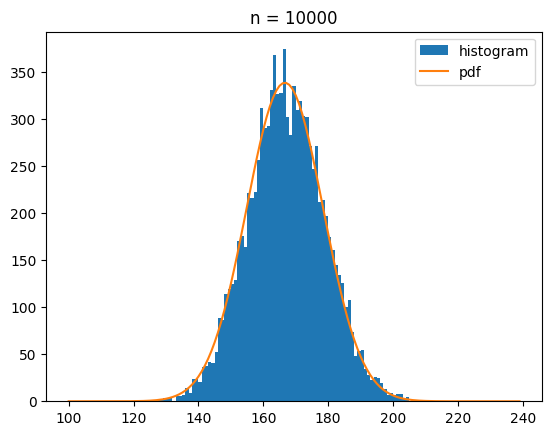
이번에는 draw_dice를 100번, 1000번, 10000번 호출했을 때 나오는 분포를 정규분포 확률 밀도 함수와 함께 시각화 해 볼게요.

bins = range(100,240)
for n in [100,1000,10000]:
  ecnt = np.array([draw_dice() for _ in range(n)])
  s_mean = ecnt.mean()
  s_std = ecnt.std()
  plt.hist(ecnt,bins=bins,label='histogram')
  y = norm.pdf(bins,s_mean,s_std)*n
  plt.plot(bins,y,label='pdf')
  plt.legend()
  plt.title(f'n = {n}')
  plt.show()

[out]