이 책에서 내용을 살펴보기로 할게요.
여기서는 통계에 관한 파이썬 모듈 중에 scipy 모듈의 하위 모듈인 stats을 사용합니다.
import scipy as sp
from scipy import stats해당 모듈에 관한 공식 문서는 다음 주소에 있습니다.
https://docs.scipy.org/doc/scipy/
https://docs.scipy.org/doc/scipy/tutorial/stats.html
분포
데이터 과학에서 다루는 데이터는 다양한 형태의 분포를 지닙니다.
크게 연속적인 분포와 불연속적인 이산 분포로 나눌 수 있는데 scipy.stats에서는 대략 100가지 분포를 다룰 수 있게 다양한 하위 모듈과 함수들을 제공합니다.
여기에서는 6가지의 연속 분포와 2가지의 불연속 분포를 다룹니다.
각 분포가 어떠한 분포인지에 관한 설명부터 구체적 사용은 각 분포에서 다룰게요.
다음은 연속 분포에서 다룰 하위 모듈들입니다.
from scipy.stats import chi2 #카이제곱분포
from scipy.stats import expon #지수 분포
from scipy.stats import f #F분포
from scipy.stats import norm #정규 분포
from scipy.stats import t #t분포
from scipy.stats import uniform #균일 분포다음은 불연속 분포에서 다룰 하위 모듈들입니다.
from scipy.stats import binom #이항 분포
from scipy.stats import poisson #포아송 분포분포에서 다루는 주요 함수
여러 분포에서 비슷한 여러 함수를 제공합니다.
원하는 분포의 샘플 데이터를 생성하거나 확률을 구하는 등의 함수 중에 다음 6가지는 이 책에서 주요하게 다룹니다.
- rvs – 랜덤 샘플 생성 함수
- pdf – 확률 밀도 함수
- cdf – 누적 분포 함수
- sf – 생존 함수
- ppf – 퍼센트 포인트 함수
- pmf 확률 질량 함수
#A집단의 평가 점수는 평균이 80, 표준편차가 5라고 한다.
#샘플 20개를 생성하시오.
norm.rvs(loc=80,scale=5,size=20) [out]
array([85.68540596, 78.94708622, 76.41693652, 78.30443218, 68.50757721,
81.12168051, 64.46056614, 80.87128425, 88.11608527, 70.33474697,
79.5365341 , 71.45992979, 84.55597935, 86.15858429, 84.24138845,
78.86059601, 77.02020931, 79.99373916, 88.21055625, 73.99369846])#A집단의 평가 점수는 평균이 80, 표준편차가 5라고 한다.
#예상 분포를 도식화하시오.
import matplotlib.pyplot as plt
x = range(0,101)
y = norm.pdf(x,80,5)
plt.plot(x,y)
plt.show()[out]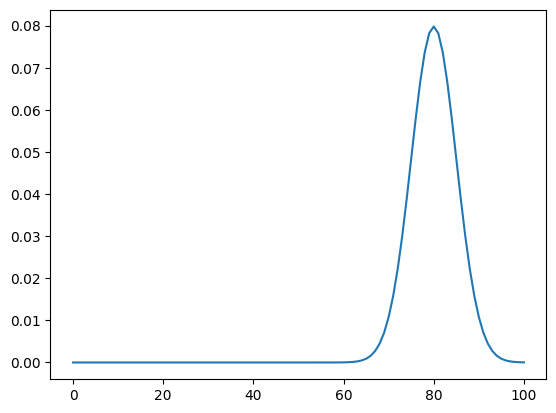
#A집단의 평가 점수는 평균이 80, 표준편차가 5라고 한다.
#75점 이하를 받을 확률을 구하시오.
norm.cdf(loc=80,scale=5,x=75)[out]
0.15865525393145707#A집단의 평가 점수는 평균이 80, 표준편차가 5라고 한다.
#75점 이상 받을 확률을 구하시오.
print(1-norm.cdf(loc=80,scale=5,x=75)) #누적 분포 함수로 구하기
print(norm.sf(loc=80,scale=5,x=75)) #생존 확률로 구하기[out]
0.8413447460685429
0.8413447460685429#A집단의 평가 점수는 평균이 80, 표준편차가 5라고 한다.
#상위 40퍼센트에 속하기 위해 받아야 하는 점수는 얼마인가?
print(norm.ppf(loc=80,scale=5,q=0.6)) #생존 확률로 구하기[out]
81.266735515679#공정한 동전을 5번 던져서 앞면이 나올 횟수가 1,2,3,4번일 확률을 소수점 이하 3자리까지 구하시오.
re = binom.pmf(n=5,p=0.5,k=[1,2,3,4])
for i in range(4):
print(i+1,'회 성공할 확률',round(re[i],3))[out]
1 회 성공할 확률 0.156
2 회 성공할 확률 0.312
3 회 성공할 확률 0.312
4 회 성공할 확률 0.156검정
이 책에서는 다음의 다양한 검정들도 다룹니다.
*검정 관련 내용을 집필한 후에 수정할게요.*
