회귀 모델 평가 도구 – 머신러닝 with 파이썬

사용할 모듈 포함문

from sklearn.metrics import r2_score #r2 결정 계수(회귀)
from sklearn.metrics import mean_absolute_error #평균 절대 오차
from sklearn.metrics import mean_squared_error #평균 제곱 오차
from sklearn.metrics import mean_absolute_percentage_error #평균 절대 퍼센트 오차
from sklearn.model_selection import cross_val_score #교차 검증 점수

from sklearn.linear_model import LinearRegression #선형 회귀
from sklearn.svm import SVR #서포트 벡터 머신 회귀
from sklearn.neighbors import KNeighborsRegressor #K 최근접 이웃 회귀
from sklearn.tree import DecisionTreeRegressor #결정 트리 회귀
from sklearn.ensemble import RandomForestRegressor #랜덤 포리스트 회귀
from sklearn.datasets import load_diabetes #당뇨병 환자 데이터 로드
from sklearn.model_selection import train_test_split #학습 및 테스트 데이터 분리
from sklearn.preprocessing import MinMaxScaler

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

회귀 모델 평가 도구

사이킷 런에서는 다양한 평가 도구를 제공하고 있습니다.

사이킷 런 평가 도구 – sklearn.metrics

사이킷 런 평가 도구 메뉴얼 사이트

사이킷 런의 회귀 모델의 기본 평가 도구는 R2 결정 계수로 r2_score로 제공하고 있습니다.

이 외에 MAE, MSE, MAPE 등이 있는데 이들에 대해 알아보기로 할게요.

여기에서는 다음의 실제 데이터(actual)와 예측 데이터(predict)가 있다고 가정하고 이를 다양한 도구로 평가해 보기로 할게요.

predict = np.array([172, 188, 177, 165, 171])
actual = np.array([170, 183, 176, 162,174])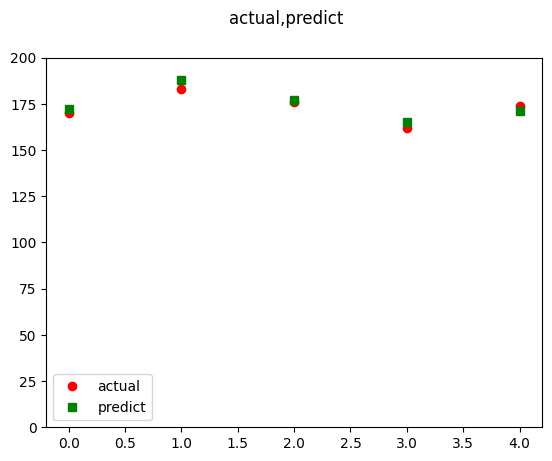

MAE

MAE는 Mean Absolute Error로 평균 절대 오차라고 부릅니다.

오차는 실제 값과 예측 값의 차이입니다.

MAE는 오차의 부호를 없애기 위해 절대값을 취한 후에 평균을 내는 것입니다.

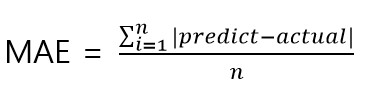
sklearn.metrics.mean_absolute_error(y_true, y_pred, *, sample_weight=None, multioutput=’uniform_average’)

mean_absolute_error 메뉴얼 사이트

직접 만든다면(만들 필요는 전혀 없지만) 다음과 같을 거예요.

def mean_absolute_error_m(actual,predict):
  return (np.abs(predict-actual)).mean()

직접 만든 함수와 사이킷 런에서 제공하는 함수로 MAE 평가를 해 봅시다.

print(f'mae:{mean_absolute_error_m(actual, predict):.3f}')
print(f'mae:{mean_absolute_error(actual, predict):.3f}')

[out]
mae:2.800
mae:2.800

평균 절대 오차 값이 2.8이네요. (평균 절대 오차 값은 작으면 좋은 결과입니다.)

사용한 표본 데이터로 보았을 때 실제 값의 범위가 160~190 정도로 볼 수 있을 거예요.

이러한 사항을 알고 있다면 평균 절대 오차 값이 큰 것인지 작은 것인지 판단할 수 있지만 실제 값의 범위를 모른다고 할 때 객관적인 판단을 하는 것은 어렵습니다.

MSE

MSE는 오차 제곱의 평균을 낸 값으로 평균 제곱 오차라고 부릅니다.

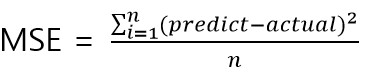
sklearn.metrics.mean_squared_error(y_true, y_pred, *, sample_weight=None, multioutput=’uniform_average’, squared=True)

mse 메뉴얼 사이트

이번에도 만들어 볼게요. (역시 전혀 만들 필요는 없습니다.)

def mean_squared_error_m(actual,predict):
  return ((predict-actual)**2).mean()

작성한 함수와 사이킷 런에서 제공하는 함수를 이용하여 평가해 봅시다.

print(f'mse:{mean_squared_error_m(actual, predict):.3f}')
print(f'mse:{mean_squared_error(actual, predict):.3f}')

[out]
mse:9.600
mse:9.600

mae 평가 결과는 2.8이었는데 mse는 9.6이네요. (평균 절대 오차 값은 작으면 좋은 결과입니다.)

mse도 mae처럼 역시 원래 값의 범위(160~190으로 추정)를 확인하지 않는다면 객관적인 평가를 하는 것은 어렵습니다.

MAPE

오차의 절대값을 실제 값으로 나눈 비율의 평균입니다.

mse나 mae와 다르게 실제 값의 범위를 확인하지 않는다고 하더라도 비교적(mse, mae에 비해) 객관적인 평가는 할 수 있겠네요.

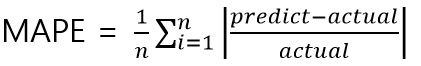
sklearn.metrics.mean_absolute_percentage_error(y_true, y_pred, *, sample_weight=None, multioutput=’uniform_average’)

mape 메뉴얼 사이트

이번에도 직접 만들어 보고 사이킷 런에서 제공하는 함수와 함께 사용해 볼게요.

def mean_absolute_percentage_error_m(actual,predict):
  return np.abs(((predict-actual)/actual)).mean()

print(f'mape:{mean_absolute_percentage_error_m(actual, predict):.3f}')
print(f'mape:{mean_absolute_percentage_error(actual, predict):.3f}')

mape:0.016
mape:0.016

mape 값이 0.016이네요. 오차는 실제 값에 비해 1/60 수준이네요.

R2 결정 계수

사이킷 런에서 회귀 모델의 기본 평가 도구는 R2 결정 계수입니다.

R2 결정 계수는 회귀 분석 결과를 보다 객관적으로 평가할 수 있는 도구입니다.

R2 결정 계수는 최대 값이 1이며 이 때가 회귀 결과가 정확함을 의미합니다.

보통 1에 근접하면 좋은 학습, 0에 가까우면 쓸모 없는 학습, 음수일 때는 욕 나오는 학습으로 볼 수 있습니다.

사이킷 런에서는 r2_score 함수를 이용합니다.

sklearn.metrics.r2_score(y_true, y_pred, *, sample_weight=None, multioutput=’uniform_average’, force_finite=True)

r2_score 메뉴얼 사이트

R2 결정 계수를 구하는 수식을 모른다고 하더라도 제공하는 r2_score 함수를 호출하면 결과를 알 수 있습니다.

하지만 보다 깊은 이해를 위해 R2 결정 계수도 어떻게 나오는 것인지 알아보고 직접 만들어 봅시다.

R2 결정 계수를 이해하기 위해 SST, SSR, SSE를 먼저 이해해야 합니다.

SST

SST는 실제 값과 평균 값의 차이를 제곱한 값들의 합입니다. 다른 말로 TSS(Totasl sum of squares)라고도 부릅니다.

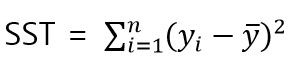
def sst(actual):
  am = actual.mean()
  return ((actual-am)**2).sum()

print(f"sst:{sst(actual)}")

[out]
sst:240.0

SSR

SSR은 잔차 제곱 합계로 RSS(Residual Sum of Squares)라고도 부릅니다.

잔차(Residual)은 실제 값과 예측 값의 차이입니다. MAE에서의 Error라고 볼 수 있습니다.

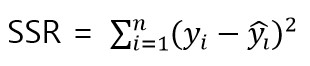
def ssr(actual, predict):
  return ((actual-predict)**2).sum()

print(f"ssr:{ssr(actual, predict)}")

[out]
ssr:48

SSE

SSE는 설명된 합계의 제곱이라는 의미로 ESS(Explained Sum of Squares)라고도 부릅니다.

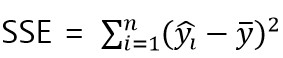
def sse(actual,predict):
  return((predict-actual.mean())**2).sum()

print(f"sse:{sse(actual, predict)}")

[out]
sse:310.0

R2 수식

R2 수식은 SSE를 SST로 나눈 값입니다.

선형 대수학에서 SST = SSR + SSE 라고 증명을 합니다. (참고: 위키 백과 Explained_sum_of_squares)

위 수식에 의해 R2 수식은 1 에서 SSR을 SST로 나눈 값을 뺀 값으로 표현할 수도 있습니다.

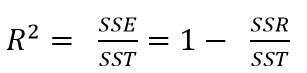
두 가지 방법으로 모두 만들어 본 후에 사이킷 런에서 제공하는 r2_score 함수 호출 결과와 비교해 봅시다.

def r2_score_m(actual, predict):
  return sse(actual, predict)/sst(actual)

def r2_score_m2(actual, predict):
  return 1 - ssr(actual, predict)/sst(actual)

print(f'r2:{r2_score_m(actual, predict):.3f}')
print(f'r2:{r2_score_m2(actual, predict):.3f}')
print(f'r2:{r2_score(actual, predict):.3f}')

[out]
r2:1.292
r2:0.800
r2:0.800

결과를 보면 두 번째 만든 함수는 같은 결과가 나오지만 첫 번째 함수는 다른 결과가 나옵니다.

첫 번째 함수의 결과도 같아야 하지만 일부 수학적 가정에 만족하지 못하는 부분이 존재합니다.

회귀 모델 학습 및 평가

이제 실제 다양한 회귀 모델로 학습한 후에 모델을 평가해 보기로 합시다.

여기에서 사용할 데이터는 공공 데이터 포털에서 2023년 6월 19일에 등록한 전국 산업 단지 현황 통계에서 필요한 항목만 추출한 데이터를 사용할 것입니다.

사용할 데이터

df = pd.read_csv('https://raw.githubusercontent.com/ehpub/ML-with-Python/main/industrial.csv')
display(df.head(3))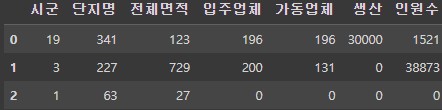

다른 항목에 의해 생산 규모를 회귀하는 실험을 해 봅시다. (R2 결정 계수만 확인해 볼게요.)

이를 위해 독립 변수와 종속 변수로 사용할 부분을 구합니다.

data = df.drop('생산',axis=1) #독립 변수
target = df['생산'] #종속 변수

학습 데이터와 테스트 데이터로 분할합시다.

여기에선 학습 데이터로 교차 검증 후에 테스트 데이터로 최종 평가하기로 할게요.

x_train,x_test, y_train,y_test = train_test_split(data,target)

다섯 종류의 회귀 모델을 생성한 후에 교차 검증을 수행합시다.

models = []
models.append(LinearRegression()) #선형 회귀 모델
models.append(SVR())  #서포트 벡터 머신
models.append(KNeighborsRegressor()) #K 최근접 이웃
models.append(DecisionTreeRegressor()) #결정 트리
models.append(RandomForestRegressor()) #랜덤 포레스트
for model in models:
  print(model.__class__.__name__,"###")
  eval_scores = cross_val_score(model,x_train, y_train)
  print(f"교차 검증 평가 점수 평균:{eval_scores.mean():.3f}")

[out]
LinearRegression ###
교차 검증 평가 점수 평균:0.319
SVR ###
교차 검증 평가 점수 평균:-0.115
KNeighborsRegressor ###
교차 검증 평가 점수 평균:0.072
DecisionTreeRegressor ###
교차 검증 평가 점수 평균:0.211
RandomForestRegressor ###
교차 검증 평가 점수 평균:0.338

실험 결과 랜덤 포레스트 모델이 다른 모델보다 나은 것으로 보이네요.

(train_test_split 함수에서는 분할할 때 랜덤하게 섞는 과정이 있기 때문에 실제 결과는 다를 수 있습니다.)

해당 모델로 최종 평가를 해 봅시다.

model = models[4]
print(model.__class__.__name__,"###")
model.fit(x_train,y_train)
predict = model.predict(x_test)
print(f"r2 결정 계수:{r2_score(y_test,predict):.3f}")

[out]
RandomForestRegressor ###
r2 결정 계수:0.181

테스트 데이터로 평가한 결과는 0.181로 교차 검증의 0.338보다 작네요.

그리고 두 값 모두 만족스러운 값은 아닙니다.

이번에는 독립 변수 부분을 MinMaxScaler로 0~1 사이의 값으로 조정 후에 해 봅시다.

mms = MinMaxScaler()
mms.fit(x_train)
x_train2 =  mms.transform(x_train)
x_test2 =  mms.transform(x_test)

다시 교차 검증 테스트를 해 볼게요.

models = []
models.append(LinearRegression())
models.append(SVR())
models.append(KNeighborsRegressor())
models.append(DecisionTreeRegressor())
models.append(RandomForestRegressor())
for model in models:
  print(model.__class__.__name__,"###")
  eval_scores = cross_val_score(model,x_train2, y_train)
  print(f"교차 검증 평가 점수 평균:{eval_scores.mean():.3f}")

[out]
LinearRegression ###
교차 검증 평가 점수 평균:0.319
SVR ###
교차 검증 평가 점수 평균:-0.115
KNeighborsRegressor ###
교차 검증 평가 점수 평균:0.017
DecisionTreeRegressor ###
교차 검증 평가 점수 평균:-0.628
RandomForestRegressor ###
교차 검증 평가 점수 평균:0.323

모델에 따라 스케일 조정 전 후의 차이가 있는 모델도 있고 그렇지 않은 모델도 있네요.

이번 테스트도 랜덤 포레스트 모델이 제일 좋은 결과를 내고 있습니다.

model = models[4]
print(model.__class__.__name__,"###")
model.fit(x_train2,y_train)
predict = model.predict(x_test2)
print(f"r2 결정 계수:{r2_score(y_test,predict):.3f}")

[out]
RandomForestRegressor ###
r2 결정 계수:0.112

최종 테스트에서도 그리 좋은 결과는 나오지 않았습니다.

실제 사용하기 위해서는 데이터를 좀 더 수집하거나 독립 변수의 특성을 변환하거나 모델의 적합한 하이퍼 파라미터를 찾는 등의 작업을 요구합니다.

여기에서는 회귀 모델 평가 도구를 소개하기 위한 목적이므로 여기까지 실험을 하기로 할게요.