사용할 모듈 포함문
import scipy as sp
from scipy import stats
from scipy.stats import binom #이항분포
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd이항분포
이항분포는 확률 p를 갖는 n번의 독립 시행에서 사건이 발생할 횟수의 분포입니다.
횟수의 분포이므로 이산 분포이며 연속 확률 분포가 아닙니다.
특히 베리누이 시행(성공 혹은 실패인 실험)의 이항 분포를 베루누이 분포라 부릅니다.
scipy 모듈의 stats.binom에서 다양한 함수를 제공합니다. [메뉴얼 사이트]
이항분포의 샘플 생성
이항분포에서도 샘플을 생성하는 함수 rvs를 제공합니다.
rvs(n, p, loc=0, size=1, random_state=None)
예를 통해 사용해 봅시다.
주사위(한 면이 나올 확률이 1/6)를 20번 던지는 실험을 100번 하였을 때 샘플 데이터를 만드시오.
확률은 p, 횟수는 n, 만들 샘플 수는 size로 전달합니다.
sample = binom.rvs(n=20,p=1/6,size=100)
print(sample)[out]
[4 1 1 2 3 2 5 4 5 7 3 5 3 2 4 1 2 3 1 5 0 4 3 2 3 3 3 3 4 3 5 1 4 4 2 5 4
7 4 5 5 5 5 1 3 1 3 4 5 3 6 4 4 2 5 3 3 5 6 2 2 1 5 4 4 4 6 3 5 3 3 1 3 6
1 2 2 1 9 6 2 5 3 0 6 2 3 2 2 4 2 2 2 5 4 4 3 1 3 3]분포를 히스토그램으로 나타내 봅시다.
lp = sample.min()
hp = sample.max()+1
plt.hist(sample,bins=range(lp,hp))
plt.title('binom.rvs(n=20,p=1/6,size=100)')
plt.show()[out]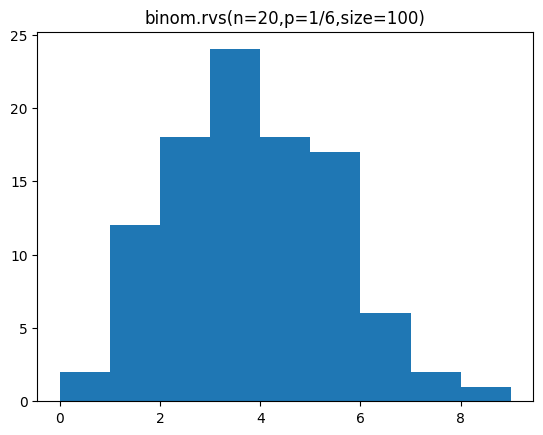
베르누이 시행과 중심 극한 정리
중심 극한 정리는 앞에서 이미 다뤘던 내용입니다.
균등 분포 확률을 갖는 독립 변수의 분포는 확률 변수의 개수가 충분히 크면 정규 분포에 가까워 진다는 것이 중심 극한 정리라고 하였습니다.
여기에서는 결과가 성공 혹은 실패인 사건의 이항분포인 베르누이 시행을 통해 중심 극한 정리를 코드로 확인해 보는 작업을 해 볼게요.
다음은 확률 p인 사건을 베르누이 시행을 size회 시행했을 때 성공 횟수를 요소로 하는 샘플을 tn개 만드는 함수를 정의한 것입니다.
def trial_bernoulli_n(p=2/1,size=10,tn=10):
tl =[]
for _ in range(tn):
sample = binom.rvs(n=1,p=p,size=size)
positive_cnt = np.unique(sample,return_counts=True)[1][1]
tl.append(positive_cnt)
return np.array(tl)trial_bernoulli_n 함수를 통해 기대 확률이 1/6인 주사위를 1000번 던졌을 때 특정 면이 나오는 횟수를 100개, 1000개, 10000개 샘플을 구하여 분포를 시각화하는 코드입니다.
size=1000
p = 1/6
exp_val = int(size*p)
bins = range(exp_val-50,exp_val+51)
for tc in [100,1000,10000]:
sample = trial_bernoulli_n(p=p,size=size,tn=tc)
plt.hist(sample,bins=bins)
plt.title(f'trial_bernoulli_n(p=1/6,size={size},tn={tc})')
plt.show()[out]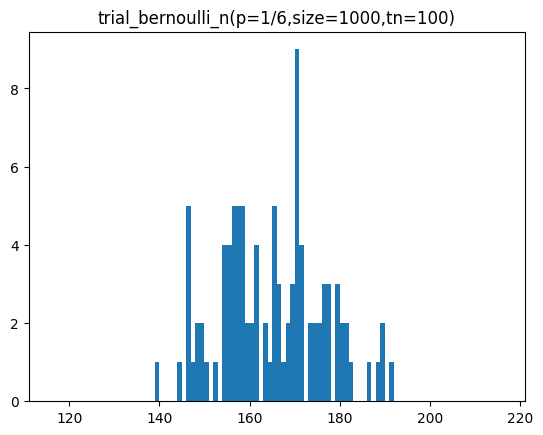
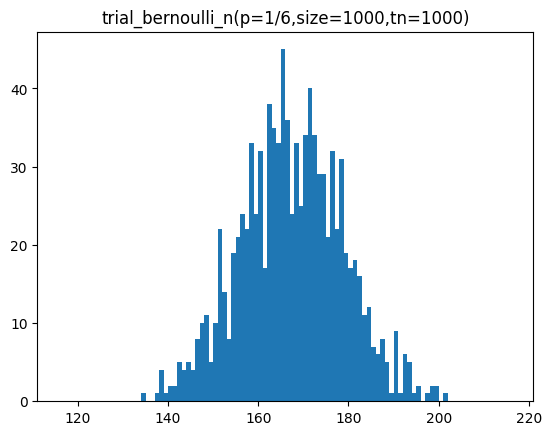
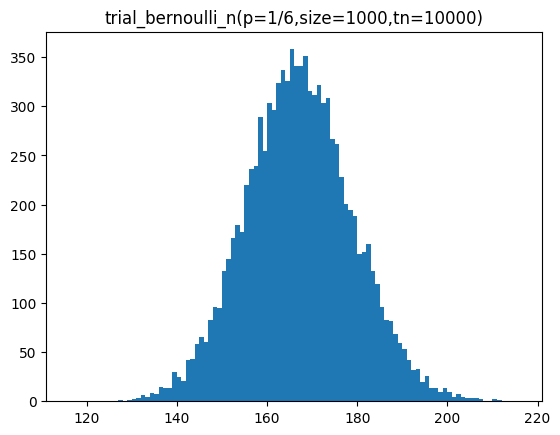
n이 커질수록 정규분포 곡선과 유사해지는 것을 볼 수 있습니다.
이항분포의 확률 질량 함수
이항분포에서 확률 질량 함수도 pmf입니다.
pmf(k, n, p, loc=0)
예를 통해 사용해 봅시다.
동전을 던져서 앞면이 나올 확률은 1/2이다.
동전을 100번 던졌을 때 나올 횟수별 확률(소수점 이하 2자리)을 구하시오.
횟수는 n, 확률은 p, 알고자 하는 확률의 횟수는 k로 전달합니다.
x = range(0,100)
y = binom.pmf(n=100,p=1/2,k=x)
print(np.round(y,2))[out]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.01 0.01 0.02
0.02 0.03 0.04 0.05 0.06 0.07 0.07 0.08 0.08 0.08 0.07 0.07 0.06 0.05
0.04 0.03 0.02 0.02 0.01 0.01 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. ]이를 횟수, 확률 도면으로 시각화해 봅시다.
plt.plot(x,y)
plt.xlabel("time")
plt.ylabel("probability")
plt.title('binom.pmf(n=100,p=1/2,k=range(0,100))')
plt.show()[out]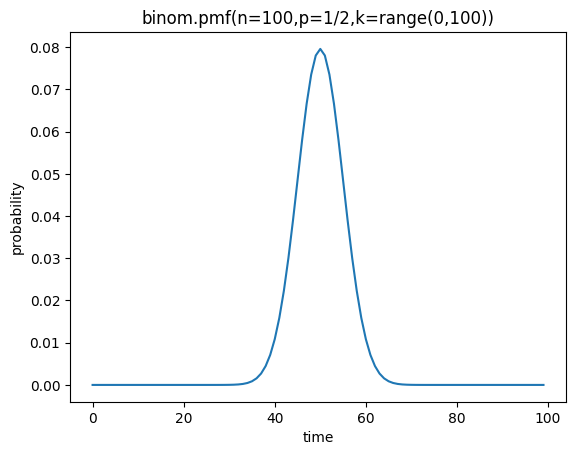
이항분포의 누적 분포 함수
이항분포의 누적 분포 함수도 cdf입니다.
cdf(k, n, p, loc=0)
예를 통해 사용해 봅시다.
동전을 던져서 앞면이 나올 확률은 1/2이다.
동전을 100번 던졌을 때 40회 이하가 나올 확률을 소수점 이하 3자리까지 구하시오.
횟수는 n, 확률은 p, 알고자 하는 확률의 횟수는 k를 전달합니다.
p = binom.cdf(n=100,p=1/2,k=40)
print(np.round(p,3))[out]
0.028이는 다음처럼 0회부터 원하는 횟수까지의 확률을 더한 값과 같습니다. (실제 소수점 이하를 고려하지 않고 값을 출력하면 메모리에 실수 표현할 때의 오차로 인해 미세하게 다를 수 있습니다.)
p=0
for i in range(41):
p += binom.pmf(n=100,p=1/2,k=i)
print(np.round(p,3))[out]
0.028동전을 100번 던졌을 때 40회 이상 70회 미만이 나올 확률을 소수점 이하 3자리까지 구하시오.
69회까지의 누적 확률에서 39회까지의 누적 확률을 빼면 40회 이상 70회 미만이 나올 확률을 구할 수 있습니다.
lp = binom.cdf(n=100,p=1/2,k=39)
hp = binom.cdf(n=100,p=1/2,k=69)
print(hp-lp)
print(np.round(hp-lp,3))[out]
0.9823606491929197
0.982다음처럼 40회부터 69회가 나올 확률을 더해서 확인해 볼 수 있습니다.
p=0
for i in range(40,70):
p += binom.pmf(n=100,p=1/2,k=i)
print(p)
print(np.round(p,3))[out]
0.9823606491929195
0.982이항분포의 생존함수
이항분포의 생존함수도 sf입니다.
sf(k, n, p, loc=0)
예를 통해 사용해 봅시다.
동전을 100번 던졌을 때 60회 이상 나올 확률을 소수점 이하 3자리까지 구하시오.
실험 횟수는 n, 확률은 p, 발생 횟수는 k로 전달합니다.
p = binom.sf(n=100,p=1/2,k=59)
print(round(p,3))[out]
0.028이는 1에서 누적 분포 확률을 뺀 값과 같습니다.
neg_p = binom.cdf(n=100,p=1/2,k=59)
print(round(1-neg_p,3))[out]
0.028물론 1에서 원하는 횟수 미만의 발생 횟수가 발생할 확률을 빼더라고 구할 수 있습니다.
p = 1
for i in range(60):
p -= binom.pmf(n=100,p=1/2,k=i)
print(round(p,3))[out]
0.028이항분포의 퍼센트 포인트 함수
이항분포의 퍼센트 포인트 함수도 ppf 입니다.
ppf(q, n, p, loc=0)
예를 통해 사용해 봅시다.
동전을 100번 던졌을 때 n회 이상 나올 확률이 80%가 처음으로 넘는다고 한다. n을 구하시오.
횟수는 n, 확률은 p, 원하는 지점의 확률은 q로 전달합니다.
n = binom.ppf(n=100,p=1/2,q=0.8)
print(int(n))[out]
54실제 결과가 맞는지 53회 이하의 확률과 54회 이하의 확률을 확인해 봅시다.
print(binom.cdf(n=100,p=1/2,k=53))
print(binom.cdf(n=100,p=1/2,k=54))[out]
0.7579407931963542
0.8158991913366521