연속 균일 분포

유튜브 동영상 강의

사용할 모듈 포함문

import scipy as sp
from scipy import stats
from scipy.stats import uniform
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

연속 균일 분포(연속 균등 분포)는 분포가 특정 범위 내에서 같게 나오는 분포를 말합니다.

파이썬의 scipy 모듈에서는 stats.uniform 으로 제공하고 있습니다. [메뉴얼 사이트]

연속 균일 분포의 예로는 버스 시간표를 모르고 버스 정류장에 나갔을 때 평균 대기 시간을 들 수 있습니다.

샘플 생성하기

rvs(loc=0, scale=1, size=1, random_state=None)

구간 시작은 loc, 구간 범위는 scale, 생성할 샘플 개수는 size 인자로 전달합니다.

다음은 연속 균일 분포 샘플을 10개 생성하는 것입니다. loc과 scale을 전달하지 않으면 디폴트 값이 0과 1이므로 0에서 1사이의 구간에서 균일한 확률로 랜덤한 값을 발급합니다.

sample = uniform.rvs(size=10)
print(sample)

[out]
[0.09541329 0.66722734 0.58454357 0.81562865 0.92742487 0.95646056
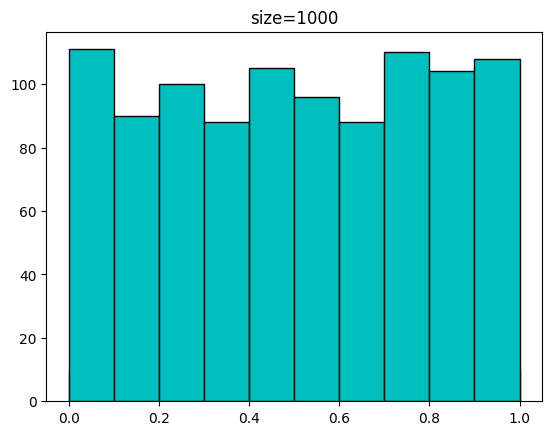
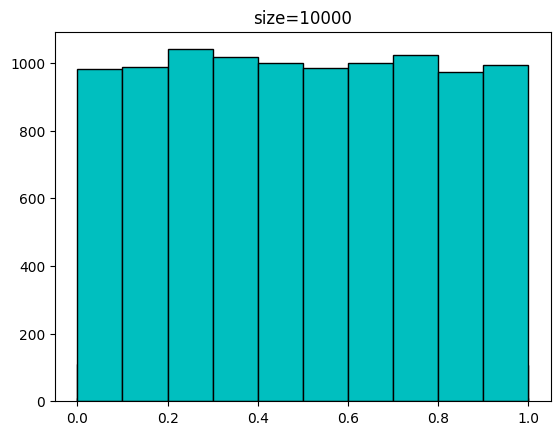
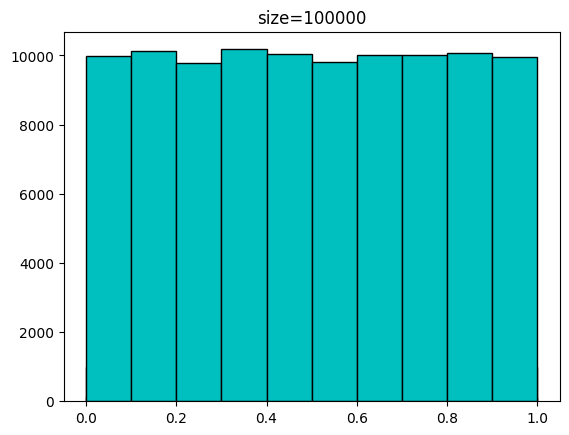
 0.37905847 0.96105773 0.90171608 0.80419579]

다음은 발급받은 샘플 개수에 따른 분포입니다.

for n in [100,1000,10000,100000]:
  sample = uniform.rvs(size=n)
  plt.hist(sample,bins=np.linspace(0,1,11),color='c',edgecolor='k')
  plt.title(f'size={n}')
  plt.show(())

[out]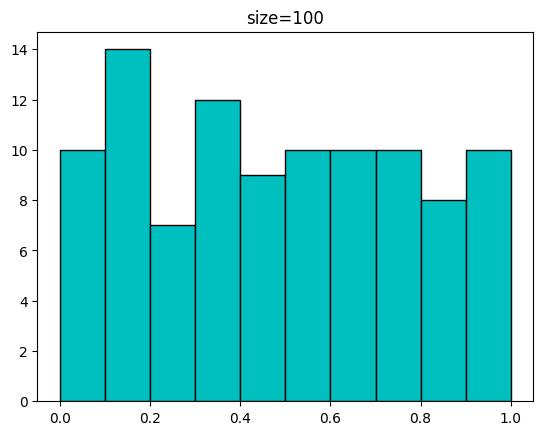

다음은 scale을 5로 설정하여 10개의 샘플을 발급받는 코드입니다. 0~5사이의 랜덤한 값을 10개 발급하겠네요.

sample = uniform.rvs(scale=5,size=10)
print(sample)

[out]
[4.7670246  4.83506854 4.26028673 3.09390333 4.36924443 1.72182815
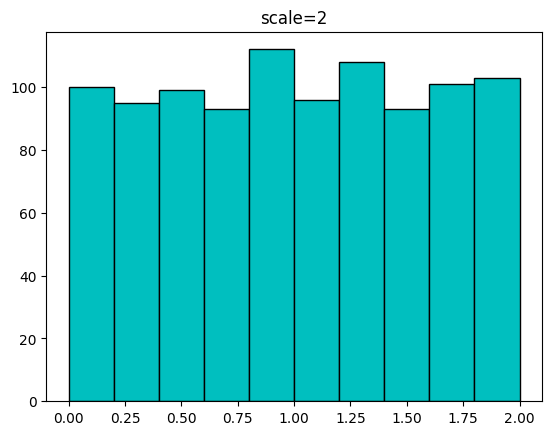
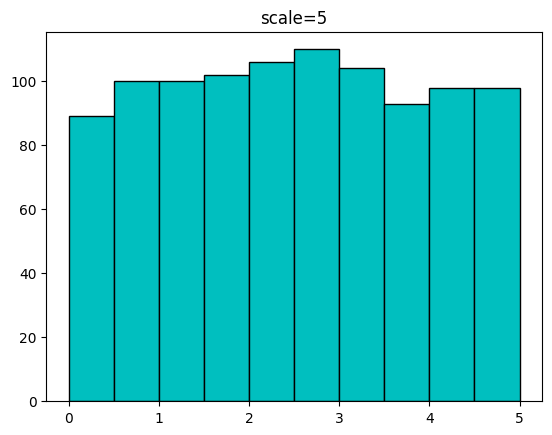
 2.49855518 0.43257482 0.89291281 2.5282866 ]

다음은 scale을 1, 2, 5를 주고 size를 1000을 주었을 때의 분포를 시각화한 코드입니다.

for s in [1,2,5]:
  sample = uniform.rvs(scale=s,size=1000)
  plt.hist(sample,bins=np.linspace(0,s,11),color='c',edgecolor='k')
  plt.title(f'scale={s}')
  plt.show()

[out]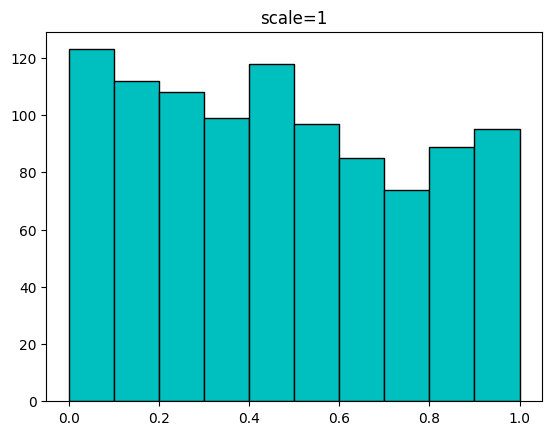

uniform.rvs(sclae=1,size=1000) 발급한 샘플 분포.png

uniform.rvs(sclae=2,size=1000) 발급한 샘플 분포.png

uniform.rvs(sclae=5,size=1000) 발급한 샘플 분포.png

확률 밀도 함수 및 누적 분포 함수

pdf(x, loc=0, scale=1) :확률 밀도 함수

cdf(x, loc=0, scale=1): 누적 분포 함수

확률 밀도 함수의 결과는 loc에서 sclae 사이일 때는 언제나 1/(scale-loc)값을 반환합니다.

구간 a,b일 때 확률 밀도 값은 1/(b-a)입니다.

pdf 함수에 loc와 sclae을 전달하지 않으면 디폴트 값이 0과 1이기 때문에 x값으로 0~1 사이의 값을 전달하면 언제나 1을 반환합니다. 이는 1/(scale-loc)값입니다.

x = np.linspace(0,1,21)
y = uniform.pdf(x=x)
plt.plot(x,y,color='r')
plt.fill_between(x,y)
plt.title('uniform.pdf')
plt.show()

[out]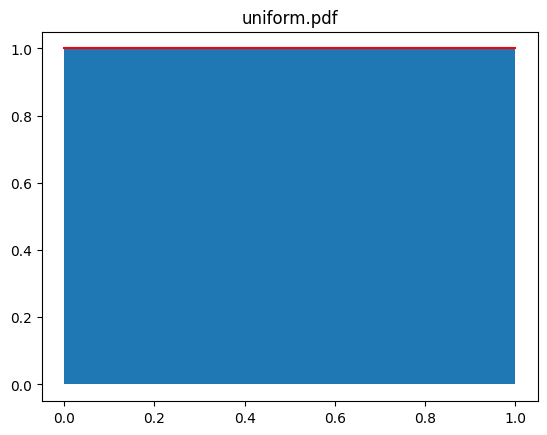

x = np.linspace(0,1,21)
y = uniform.cdf(x=x)
plt.plot(x,y,color='r')
plt.fill_between(x,y)
plt.title('uniform.cdf')
plt.show()

[out]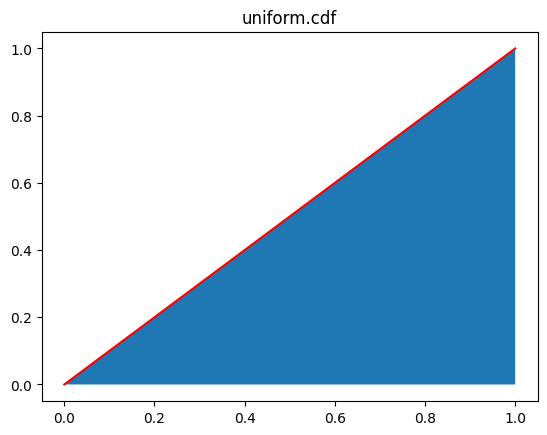

예를 통해 좀 더 알아볼게요.

A마을에 마을 버스는 1시간 주기로 다닌다고 한다. 버스 시간표를 모르는 사람이 A마을 버스 정류장에 갔을 때 대기시간이 7분 이내일 확률을 구하시오.

주기가 60분이므로 scale을 60을 전달할게요. 7분 이내일 확률이므로 x를 7을 주어 cdf 함수를 호출합니다.

y = uniform.cdf(scale=60,x=7)
print(y)

[out]
0.11666666666666667

scale을 디폴트 1(시간)으로 주고 x를 7/60을 전달할 수도 있겠죠.

y = uniform.cdf(x=7/60)
print(y)

[out]
0.11666666666666667

대기시간이 5분에서 20분 이내일 확률을 구하시오.

ly = uniform.cdf(scale=60,x=5)
hy = uniform.cdf(scale=60,x=20)
print("대기시간이 5분에서 20분 이내일 확률은 ",hy-ly)

[out]
대기시간이 5분에서 20분 이내일 확률은  0.25

대기시간이 50분 이내 및 초과할 확률을 구하시오.

y1 = uniform.cdf(scale=60,x=50)
y2 = uniform.sf(scale=60,x=50)
print("대기시간이 50분 이내일 확률은 ",y1)
print("대기시간이 50분 초과할 확률은 ",y2) #y2 = 1-y1

[out]
대기시간이 50분 이내일 확률은  0.8333333333333334
대기시간이 50분 초과할 확률은  0.16666666666666663

대기시간이 m분 이내일 확률이 73%라고 한다. m은 얼마인지 구하시오.

m = uniform.ppf(scale=60,q=0.73)
print(f"대기 시간이 {m}분 이내일 확률은 73%")

[out]
대기 시간이 43.8분 이내일 확률은 73%