사용할 모듈 포함
from sklearn.linear_model import LinearRegression #선형 회귀
from sklearn.metrics import mean_squared_error #평균 제곱 오차
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt선형 회귀 모델
선형 회귀 모델은 독립 변수와 종속 변수 사이의 선형 관계를 찾아 회귀식(선형 회귀 함수)을 통해 예측하는 모델입니다.
모델 학습 과정에서 찾은 선형 관계를 예측에 사용하며 선형 관계를 표현한 회귀식을 선형 회귀 함수라고 부릅니다.
선형 회귀 함수
선형 회귀 함수는 독립 변수의 각 특성이 종속 변수에 영향을 주는 정도인 가중치와 편향으로 구성합니다.

머신러닝 모델이 학습 과정에서 알아낸 값으로 예측에 사용하는 값들을 모델 파리미터라고 부릅니다.
선형 회귀 모델에서 모델 파라마터는 가중치(weight)와 편향(bias)이 있습니다.
일반적으로 머신러닝의 복잡도는 모델 파라미터의 개수와 비례합니다.
사용할 데이터
선형 회귀 모델과 경사 하강법을 설명할 때 사용할 데이터를 먼저 소개할게요.
x_src = np.arange(-10,10,0.5)
y_src = np.array([-15., -13., -15., -10., -11., -18., -10., -7., -13., -12., -3.,
-8., -7., -2., 1., -2., 1., 1., 9., 3., 11., 2.,
5., 2., 14., 13., 12., 12., 15., 8., 17., 12., 14.,
14., 14., 14., 18., 17., 19., 25] )다음은 사용할 데이터를 도면에 표식한 것입니다.
plt.figure(figsize=(6,6))
plt.plot(x_src,y_src,'ro')
plt.axvline(x=0,color='k')
plt.axhline(y=0,color='k')
plt.xlim(-20,20)
plt.ylim(-20,20)
plt.show()[out]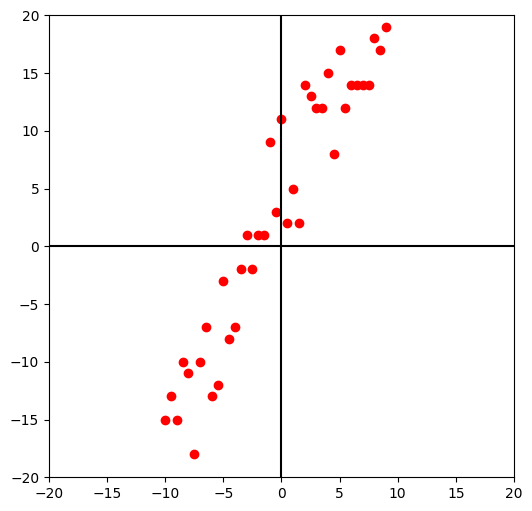
다음은 사용할 데이터와 세 개의 직선을 도식한 것인데 세 개의 직선 중에 사용할 데이터를 가장 잘 표현하는 직선은 무엇인가요?
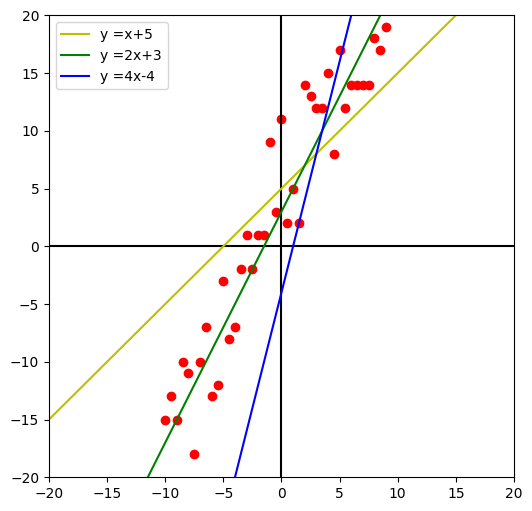
녹색 선으로 표현한 y = 2x +3 이 세 개의 직선 중에는 데이터를 잘 설명한다고 할 수 있겠네요.
이는 실제 값과 직선과의 거리가 적어 오차가 작기 때문일 것입니다.
선형 회귀 모델에서는 학습 과정에서 독립 변수와 종속 변수 사이의 선형 관계를 파악하여 모델 파라미터(가중치와 편향)을 결정합니다.
선형 회귀 함수는 학습 과정에서 결정한 모델 파라미터(가중치와 편향)에 의해 식이며 예측할 때 이를 이용합니다.
LinearRegression
class sklearn.linear_model.LinearRegression(*, fit_intercept=True, copy_X=True, n_jobs=None, positive=False)
LinearRegression 메뉴얼 사이트
사이킷 런의 대표적인 선형 회귀 모델은 LinearRegression입니다.
선형 회귀 모델로 학습하여 결정한 모델 파라미터(가중치와 편향)를 살펴보면서 얘기해 봅시다.
먼저 사용할 데이터를 모델에서 사용할 수 있는 구조로 변경할게요.
독립 변수는 여러 개의 특성으로 구성할 수 있어서 (샘플,독립변수) 구조를 갖는 2차원 구조로 변경합니다.
x = x_src.reshape(-1,1)
y = y_src
print(f'독립 변수 구조:{x.shape}, 종속 변수 구조:{y.shape}')[out]
독립 변수 구조:(40, 1), 종속 변수 구조:(40,)모델을 생성하고 학습 전에 가중치와 편향을 확인해 볼게요.
LinearRegression 모델의 모델 파라미터는 coef_(가중치)와 intercept_(편향)입니다.
model = LinearRegression() #모델 생성
print(f'가중치:{model.coef_} 편향:{model.intercept_}')---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
<ipython-input-20-1f1e96432360> in <cell line: 1>()
----> 1 print(f'가중치:{model.coef_} 편향:{model.intercept_}')
AttributeError: 'LinearRegression' object has no attribute 'coef_'보시는 것처럼 학습 전에는 coef_ 멤버가 없다는 오류를 나타내고 있습니다.
물론 학습 전에는 intercept_ 멤버도 없는 상태입니다.
이번에는 학습 후에 가중치와 편향을 확인해 봅시다.
model.fit(x,y)
print(f'가중치:{np.round(model.coef_,2)} 편향:{model.intercept_:.2f}')[out]
가중치:[1.91] 편향:3.65학습 후에는 정상적으로 가중치와 편향에 접근할 수 있습니다.
학습에 의해 결정한 모델 파라미터로 선형 회귀 함수를 도면에 도식해 볼게요.
선형 회귀 함수를 표현할 직선의 끝점은 도면의 x범위의 시작과 끝인 -20과 20으로 정할게요.
끝점의 y값은 학습한 가중치와 편향을 수식 y = wx+b에 의해 결정합니다.
xbs = np.array([-20,20])
ymin = -20*model.coef_[0] +model.intercept_
ymax = 20*model.coef_[0] +model.intercept_
ybs = np.array([ymin,ymax ])
plt.figure(figsize=(6,6))
plt.plot(x_src,y_src,'ro')
plt.axvline(x=0,color='k')
plt.axhline(y=0,color='k')
plt.plot(xbs,ybs,'b',label=f'y ={model.coef_[0]:.2f}x{model.intercept_:+.2f}')
plt.xlim(-20,20)
plt.ylim(-20,20)
plt.legend()
plt.show()[out]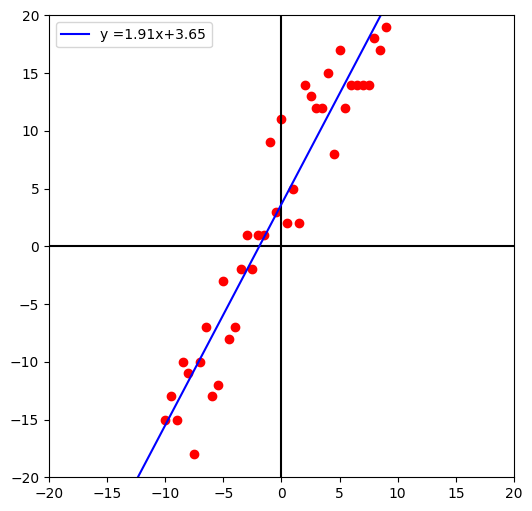
이번에는 학습한 LinearRegression 모델 개체로 예측해 볼게요.
예측에 사용할 독립 변수는 -20과 20으로 할게요.
x_test = xbs.reshape(-1,1) #(모델,독립변수) 구조로 변경
pred = model.predict(x_test)
print(f'pred:{np.round(pred,2)}')
print(f'ybs :{np.round(ybs,2)}')[out]
pred:[-34.64 41.95]
ybs :[-34.64 41.95]예측 결과는 선형 회귀 함수에 의해 계산한 값과 같음을 알 수 있습니다.
이를 통해 선형 회귀 모델은 학습 후에 결정한 모델 파라미터에 의해 결과를 예측한다는 것을 알 수 있습니다.
경사하강법을 이용하여 선형 회귀 모델 만들기
이번에는 선형 회귀 모델을 보다 깊이 이해하기 위해 직접 만들어 보기로 합시다.
여기에서는 경사하강법을 이용한 선형 회귀 모델을 만드는 실습을 할게요.
선형 회귀 모델은 학습 과정에서 어떠한 모델 파라미터가 좋은 값인지 판별할까요?
LinearRegression 모델에서는 평균 제곱 오차 값을 최소로 하는 모델 파라미터를 좋은 값으로 판단합니다.
현재 학습한 모델로 예측했을 때 평균 제곱 오차를 구해 봅시다.
pred = model.predict(x)
print(f'mse:{mean_squared_error(y,pred):.3f}')[out]
mse:11.827
사이킷 런에서는 mean_squared_error 함수로 제공하고 있는데 직접 만들어 봅시다.
(만들어야 할 이유는 1도 없습니다. 여기에서는 보다 깊은 이해를 위해 쓸모는 없지만 만들어 볼게요.)
def mse(actual,pred):
return np.sum((actual-pred)**2)/len(actual)print(f'mse:{mse(y,pred):.3f}')[out]
mse:11.827만든 mse 함수 호출 결과는 사이킷 런의 mean_squared_error 함수 호출 결과와 같다는 것을 알 수 있습니다.
이번에는 특정 가중치와 편향에서의 mse값을 구해봅시다.
여기에서는 세 개의 선형 회귀 함수의 가중치, 편향 값으로 알아볼게요.
params = [[1,5],[2,3],[4,-4]]
for w,b in params:
pr = np.array([w*e + b for e in x.reshape(-1)])
print(f'w:{w:2d} b:{b:2d} mse:{mse(y,pr):.3f}')[out]
w: 1 b: 5 mse:42.175
w: 2 b: 3 mse:12.525
w: 4 b:-4 mse:223.525결과를 보면 세 개의 선형 회귀 함수 중에서는 가중치가 2이고 편향이 3일 때 mse값이 최소임을 알 수 있습니다.
앞에서도 확인했듯이 세 개의 직선 중에는 y=2x+3이 데이터를 가장 잘 설명한다고 볼 수 있네요.

- 가중치에 따른 mse 변화
이번에는 가중치에 따라 mse 결과가 어떠한 특징을 갖는지 확인해 봅시다.
편향은 모델 학습에 의해 결정한 값으로 고정할게요.
b = model.intercept_
ws = np.arange(-10,10,0.1)
preds = np.array([[w *e + b for e in x.reshape(-1)] for w in ws])
mses =np.array([ mse(y,p) for p in preds])
mi = np.argmin(mses)
plt.figure(figsize=(4,4))
plt.plot(ws,mses)
plt.plot(ws[mi],mses[mi],'ro',label=f'w={ws[mi]:.2f}')
plt.xlabel('weight')
plt.ylabel('mse')
plt.legend()
plt.show()[out]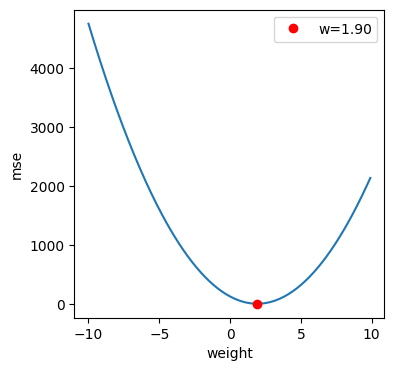
가중치와 mse의 관계는 2차 함수 관계의 곡선 형태를 지니고 있습니다.
곡선에서 맨 아래쪽이 mse의 최솟값이며 학습을 통해 이를 결정합니다.
- 편향에 따른 mse 변환
이번에는 편향에 따라 mse 결과가 어떠한 특징을 갖는지 확인해 봅시다.
가중치 모델 학습에 의해 결정한 값으로 고정할게요.
w = model.coef_[0]
bs = np.arange(-10,10,0.1)
preds = np.array([[w *e + b for e in x.reshape(-1)] for b in bs])
mses =np.array([ mse(y,p) for p in preds])
mi = np.argmin(mses)
plt.figure(figsize=(4,4))
plt.plot(bs,mses)
plt.plot(bs[mi],mses[mi],'ro',label=f'b={bs[mi]:.2f}')
plt.xlabel('bias')
plt.ylabel('mse')
plt.legend()
plt.show()[out]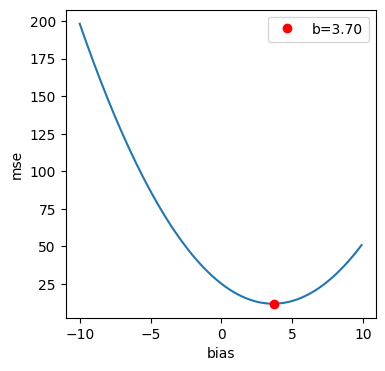
편향과 mse의 관계도 2차 함수 곡선 형태를 지니고 있네요.
마찬가지로 곡선의 맨 아래쪽이 mse 최솟값입니다.
경사하강법
경사하강법은 2차 곡선에서 기울기가 양수이면 왼쪽, 음수이면 오른쪽으로 이동하면 바닥을 만날 수 있다는 것입니다.
기울기는 미분을 통해 알 수 있죠.
가중치와 mse 사이의 미분, 편향과 mse 사이의 미분 값을 구하는 수식을 알아봅시다.
- mse 수식
mse 수식은 다음과 같이 전개할 수 있습니다.
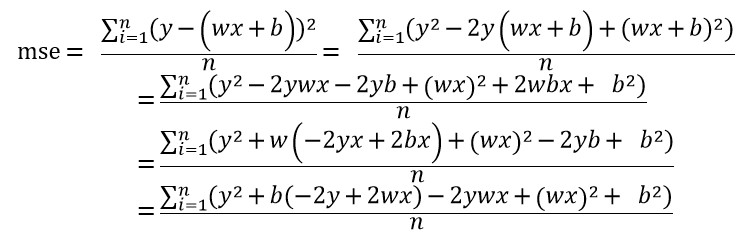
- dmse/dw 수식
mse와 가중치(w) 사이의 미분 값을 구하는 수식은 다음과 같습니다.
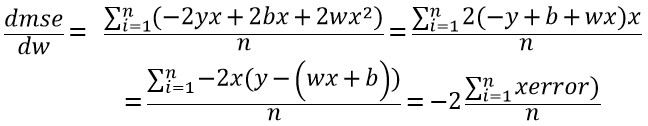
- dmse/db 수식
mse와 편향(b) 사이의 미분 값을 구하는 수식은 다음과 같습니다.
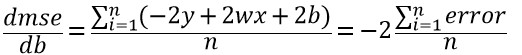
이제 기울기를 구하는 함수를 수식에 맞게 구현합시다.
def gradient(x,y,w,b):
pred = w*x + b
error = y - pred
n = len(y)
wg = -2*sum(x*error)/n
bg = -2*sum(error)/n
return wg,bg,mse(y,pred)랜덤한 가중치와 편향을 초기값으로 지정한 후에 기울기를 구하여 경사 아래로 이동이 가능한 지 실험해 봅시다.
이동할 정도는 기울기x학습률(learning rate)로 정할게요. 학습률이 작으면 조금씩 이동하고 크면 많이 이동하겠죠.
xr = x.reshape(-1)
b = np.random.uniform(-1,1)
w = np.random.uniform(-1,1)
lr = 0.01
print(f'학습률:{lr}')
print(f'시작 w:{w:.3f} b:{b:.3f} ')
wg, bg, mse_val = gradient(xr,y,w,b)
print(f'w기울기:{wg:.3f} b기울기:{bg:.3f} {mse_val:.3f}')[out]
학습률:0.01
시작 w:-0.194 b:-0.205
w기울기:-138.834 b기울기:-6.663 171.070초기에 랜덤하게 설정한 가중치와 편향에서의 mse값은 171.070입니다.
이번에는 가중치와 편향을 기울기x학습률만큼 뺀 후에 확인해 봅시다.
w = w - lr*wg
b = b - lr*bg
print(f'w:{w:.3f} b:{b:.3f} ')
wg, bg, mse_val = gradient(xr,y,w,b)
print(f'w기울기:{wg:.3f} b기울기:{bg:.3f} {mse_val:.3f}')[out]
w:1.194 b:-0.138
w기울기:-46.196 b기울기:-7.224 42.165수정한 가중치와 편향에서의 mse 값은 42.165로 많이 줄었네요.
다시 한 번 가중치와 편향을 기울기x학습률만큼 뺀 후에 확인해 봅시다.
w = w - lr*wg
b = b - lr*bg
print(f'w:{w:.3f} b:{b:.3f} ')
wg, bg, mse_val = gradient(xr,y,w,b)
print(f'w기울기:{wg:.3f} b기울기:{bg:.3f} {mse_val:.3f}')[out]
w:1.656 b:-0.066
w기울기:-15.396 b기울기:-7.310 27.413다시 수정한 가중치와 편향에서의 mse 값은 27.413로 많이 줄었네요.
다시 한 번 가중치와 편향을 기울기x학습률만큼 뺀 후에 확인해 봅시다.
w = w - lr*wg
b = b - lr*bg
print(f'w:{w:.3f} b:{b:.3f} ')
wg, bg, mse_val = gradient(xr,y,w,b)
print(f'w기울기:{wg:.3f} b기울기:{bg:.3f} {mse_val:.3f}')[out]
w:1.810 b:0.007
w기울기:-5.156 b기울기:-7.241 25.299다시 수정한 가중치와 편향에서의 mse 값은 25.299로 줄었네요.
이와 같은 형태로 점점 수정하면 곡선 아래 지점의 w,b를 구할 수 있을 것 같습니다.
이를 함수로 구현해 봅시다.
함수에서는 가중치와 편향 조절을 몇 번 할 것인지 steps를 추가합시다.
그리고 step 초기(0,1,2,3,4)와 매 100번마다 수정한 가중치와 편향 및 mse 값을 히스토리로 보관하여 최종 w,b와 함께 반환하기로 할게요.
def gradient_desent(x,y,lr=0.001,steps=10000):
w = np.random.uniform(-1,1)
b = np.random.uniform(-1,1)
hist=[]
for i in range(steps):
wg,bg,mse_val = gradient(x,y,w,b)
if (i<5)|(i%100==0):
hist.append([i,w,b,mse_val])
w = w - wg*lr
b = b - bg*lr
return w,b,hist이제 이를 이용하여 선형 회귀 함수를 구한 후 mse 값을 구해 봅시다.
w,b,hist = gradient_desent(xr,y)
print(f'w:{w:.3f} b:{b:.3f}')
pred = w*xr + b
print(mse(y,pred))[out]
w:1.915 b:3.654
11.826615853658534결과를 보면 LinearRegression 결과와 차이가 없음(혹은 비슷)을 알 수 있습니다.
경사하강법으로 구한 선형 회귀 함수를 도면에 표시합시다.
xbs = np.array([-20,20])
ymin = -20*w + b
ymax = 20*w + b
ybs = np.array([ymin,ymax ])
plt.figure(figsize=(6,6))
plt.plot(x_src,y_src,'ro')
plt.axvline(x=0,color='k')
plt.axhline(y=0,color='k')
plt.plot(xbs,ybs,'b',label=f'y ={w:.2f}x{b:+.2f}')
plt.xlim(-20,20)
plt.ylim(-20,20)
plt.legend()
plt.show()[out]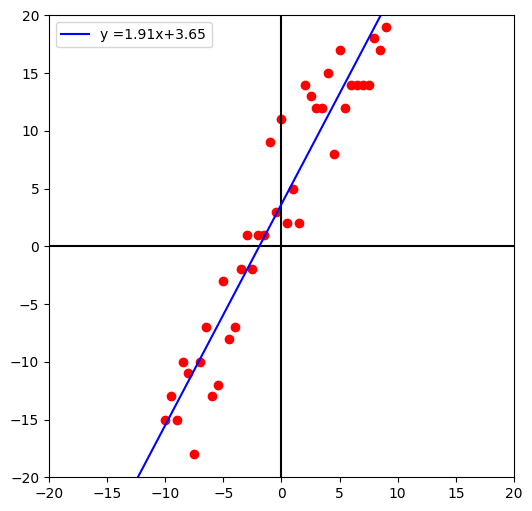
학습 히스토리를 도면에 표현해 봅시다.
step을 x축으로 하고 mse, weight, bias를 y축으로 하는 3개의 도면을 그립시다.
steps = [i for i,_,_,_ in hist]
mses = [mv for _,_,_,mv in hist]
weights = [weight for _,weight,_,_ in hist]
biases = [bias for _,_,bias,_ in hist]
fig, axs = plt.subplots(ncols=3,figsize=(12,4))
axs[0].plot(steps,mses)
axs[0].set_xlabel('step')
axs[0].set_ylabel('mse')
axs[1].plot(steps,weights)
axs[1].set_xlabel('step')
axs[1].set_ylabel('weight')
axs[2].plot(steps,biases)
axs[2].set_xlabel('step')
axs[2].set_ylabel('biases')
plt.suptitle("study history")
plt.show()[out]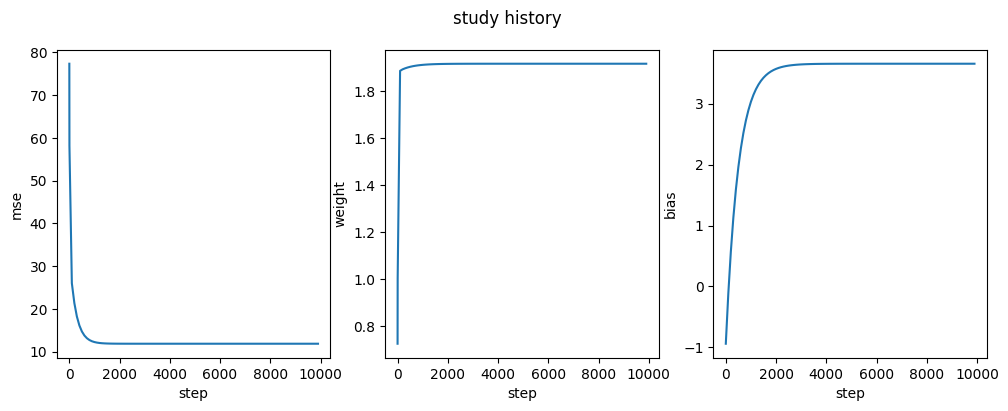
결과를 보면 step이 진행하면서 mse는 줄어드는 것을 확인할 수 있고 weight와 bias도 결정한 값으로 점점 변하는 것을 알 수 있습니다.
이미 만들어진 LinearRegression 모델을 사용하는 것으로 만족할 수 있지만 학습 과정에서 보다 깊은 이해를 위해 이와 같이 모델의 주요 알고리즘을 표현해 보는 것도 개발자의 근력 향상에 도움을 줄 것이라 생각합니다.
이상으로 선형 회귀 모델과 경사하강법에 관한 내용을 마칠게요.
