사용할 모듈 포함문
from sklearn.linear_model import LinearRegression #선형 회귀
from sklearn.preprocessing import PolynomialFeatures #다항 특성
from sklearn.model_selection import train_test_split #학습 및 테스트 데이터 분리
from sklearn.metrics import r2_score #r2 결정 계수(회귀)
from sklearn.model_selection import cross_val_score #교차 검증 점수
from sklearn.linear_model import Lasso #라쏘 L1규제
from sklearn.linear_model import Ridge #릿지 L2규제
from sklearn.linear_model import ElasticNet #엘라스틱 넷 L1+L2 규제
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings #경고
warnings.filterwarnings('ignore') #경고 무시하기규제 (Regularization)
선형 모델이 학습 데이터에 민감하게 학습하였을 때 과적합(오퍼 피팅) 현상이 발생할 수 있습니다.
이는 학습 데이터의 예측 결과는 좋으나 다른 데이터의 예측 결과는 나쁘게 나오는 현상을 말합니다.
선형 모델에서는 규제를 통해 이런 현상을 줄이는 시도를 할 수 있습니다.
규제는 원래 예측값에 패널티를 추가합니다.
여기에서 패널티는 원래 선형 회귀 함수에 의한 예측값에 잡음(패널티)을 넣어 왜곡시킨 예측값을 정하는 것입니다.
선형 모델에서는 크게 Lasso(L1 규제), Ridge(L2 규제), 엘라스틱 넷(L1+L2 규제) 등이 있습니다.
과적합(오버피팅)
다항 회귀를 다루었던 2022에 배포한 지하철 대기 데이터를 이용하여 초미세먼지를 예측을 예로 들기로 할게요.
path = 'https://raw.githubusercontent.com/ehpub/ML-with-Python/main/subway_air_2022.csv'
df = pd.read_csv(path,encoding='cp949')
df.info()[out]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 263 entries, 0 to 262
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 연번 263 non-null int64
1 호선 263 non-null object
2 역명 263 non-null object
3 미세먼지 263 non-null float64
4 초미세먼지 263 non-null float64
5 이산화탄소 263 non-null int64
6 폼알데하이드 263 non-null float64
7 일산화탄소 263 non-null float64
8 데이터기준일자 263 non-null object
dtypes: float64(4), int64(2), object(3)
memory usage: 18.6+ KB이전 실습처럼 미세먼지, 일산화탄소, 폼알데하이드, 이산화탄소 수치를 통해 초미세먼지를 예측하기로 할게요.
시각적으로 확인하기 쉽게 50개의 데이터만 사용합시다.
data = df[['미세먼지','일산화탄소','폼알데하이드','이산화탄소']].values[:50]
target = df['초미세먼지'][:50].values
x_train, x_test, y_train, y_test = train_test_split(data,target)
print(y_train.shape, y_test.shape)[out]
(37,) (13,)4차 방정식으로 특성 변환하여 학습 및 예측해 볼게요.
과적합을 확인하기 위해 예측은 학습 데이터와 테스트 데이터 모두를 수행합시다.
d = 4
pf = PolynomialFeatures(degree=d,include_bias=False)
pf.fit(x_train)
x_train_p =pf.transform(x_train)
x_test_p =pf.transform(x_test)
model = LinearRegression()
model.fit(x_train_p,y_train)
pred_train = model.predict(x_train_p)
pred_test = model.predict(x_test_p)시각적으로 보기 편하게 하기 위해 학습 관련 데이터를 DataFrame으로 만든 후에 종속 변수(초미세먼지)를 기준으로 정렬하기로 할게요.
df_train = pd.DataFrame(x_train,columns = ['미세먼지','일산화탄소','폼알데하이드','이산화탄소'])
df_train['target'] = y_train
df_train['pred'] =pred_train
df_train = df_train.sort_values(by='target')
df_train = df_train.reset_index()이제 시각화 해 봅시다.
plt.plot(df_train['target'],'bo',label='actual')
plt.plot(df_train['pred'],'r.',label='pred')
plt.legend()
plt.title(f'r2 = {r2_score(y_train,pred_train)}')
plt.show()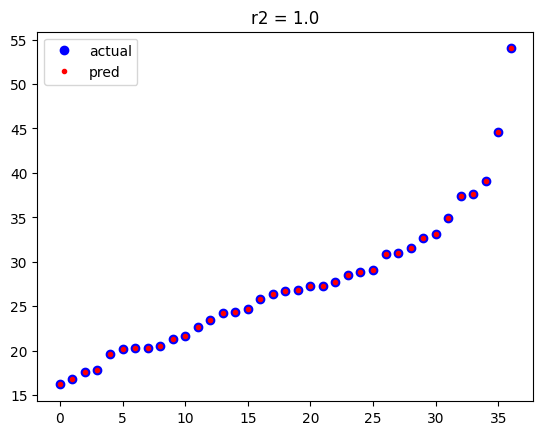
시각화 결과를 보면 알 수 있듯이 학습 데이터와 예측 값이 일치하는 것을 알 수 있습니다.
R2 결정 계수가 1이네요.
이번에는 테스트 데이터에 관한 부분도 DataFrame으로 만들고 종속 변수(초미세먼지)로 정렬합시다.
df_test = pd.DataFrame(x_test,columns = ['미세먼지','일산화탄소','폼알데하이드','이산화탄소'])
df_test['target'] = y_test
df_test['pred'] =pred_test
df_test = df_test.sort_values(by='target')
df_test = df_test.reset_index()시각화 합시다.
plt.plot(df_test['target'],'bo',label='actual')
plt.plot(df_test['pred'],'r.',label='pred')
plt.legend()
plt.title(f'r2 = {r2_score(y_test,pred_test)}')
plt.show()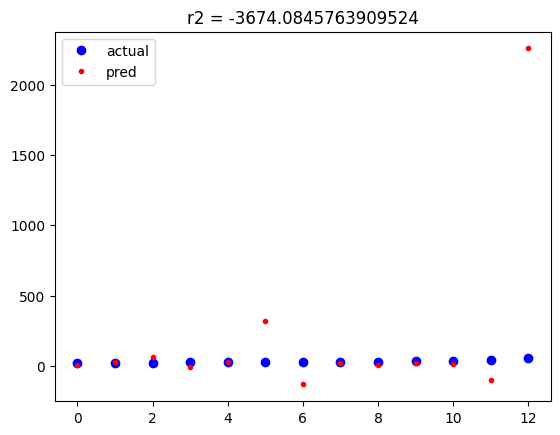
테스트 데이터는 보는 것 처럼 실제 값과 오차가 매우 큰 것들이 존재하고 있습니다.
워낙 오차가 커서 실제 값(테스트 데이터)이 수평 선 상에 있는 것처럼 보일 정도입니다.
규제에 따른 패널티
- 선형 회귀 모델의 손실 함수
규제를 적용하지 않은 선형 회귀에서는 MSE(Mean Squared Error) 값이 최소인 가중치(w)와 편향(b)을 찾습니다.
loss function = MSE
- 규제를 적용한 선형 회귀 모델
규제는 MSE에 패널티(Penalty)를 부여한 값이 최소인 가중치(w)와 편향(b)을 찾습니다.
loss function = MSE + Penalty
규제 종류는 패널티를 부여하는 방법에 따릅니다.
- Lasso(L1 규제)
패널티가 가중치 합계에 알파값을 곱한 값입니다.
알파값은 패널티 규모를 정하기 위한 값으로 0이면 규제가 없는 것입니다.
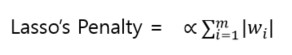
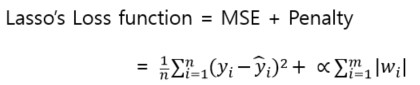
- Ridge(L2 규제)
패널티가 가중치 제곱의 합계에 알파값을 곱한 값입니다.
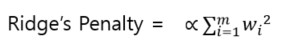
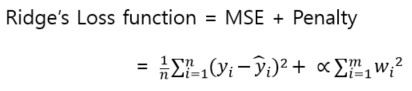
- Elastic-Net(L1 + L2 규제)
패널티가 라쏘와 리지의 패널티 합계입니다.
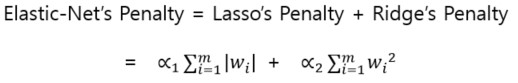
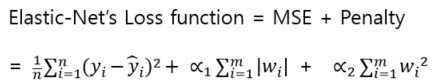
Lasso 모델로 실험
라쏘 모델로 같은 실험(미세먼지, 일산화탄소, 폼알데하이드, 이산화탄소 수치를 통해 초미세먼지를 예측)을 해 봅시다.
여기에서는 4차 방정식에 맞게 특성 변환하고 Lasso 모델로 학습 후에 학습 데이터와 평가 데이터로 예측하는 작업을 합니다.
d = 4
pf = PolynomialFeatures(degree=d,include_bias=False)
pf.fit(x_train)
x_train_p =pf.transform(x_train)
x_test_p =pf.transform(x_test)
model = Lasso()
model.fit(x_train_p,y_train)
pred_train = model.predict(x_train_p)
pred_test = model.predict(x_test_p)학습 데이터와 예측 값을 DataFrame으로 만들어 종속 변수(초미세먼지)로 정렬합시다.
df_train = pd.DataFrame(x_train,columns = ['미세먼지','일산화탄소','폼알데하이드','이산화탄소'])
df_train['target'] = y_train
df_train['pred'] =pred_train
df_train = df_train.sort_values(by='target')
df_train = df_train.reset_index()시각화해 봅시다.
plt.plot(df_train['target'],'bo',label='actual')
plt.plot(df_train['pred'],'r.',label='pred')
plt.legend()
plt.title(f'r2 = {r2_score(y_train,pred_train)}')
plt.show()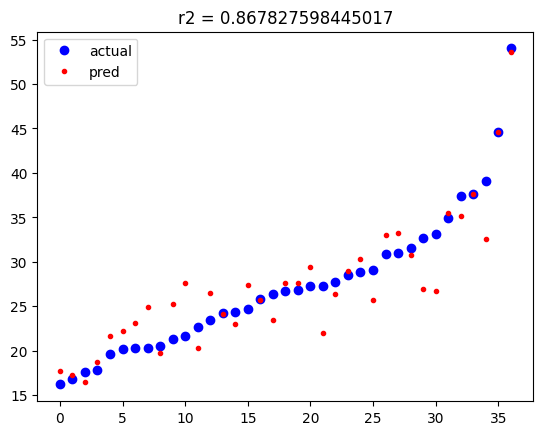
규제를 적용하기 전에는 학습 데이터와 일치하는 예측값을 보였었죠.
규제를 적용한 결과를 보면 예측값은 학습 데이터와 다소 차이가 있음을 알 수 있습니다. 이는 규제(패널티)로 인한 차이입니다.
왜 이런 패널티(잡음)을 일부러 넣었을까요?
테스트 데이터 부분도 한 번 확인해 보죠.
df_test = pd.DataFrame(x_test,columns = ['미세먼지','일산화탄소','폼알데하이드','이산화탄소'])
df_test['target'] = y_test
df_test['pred'] =pred_test
df_test = df_test.sort_values(by='target')
df_test = df_test.reset_index()시각화 해 봅시다.
plt.plot(df_test['target'],'bo',label='actual')
plt.plot(df_test['pred'],'r.',label='pred')
plt.legend()
plt.title(f'r2 = {r2_score(y_test,pred_test)}')
plt.show()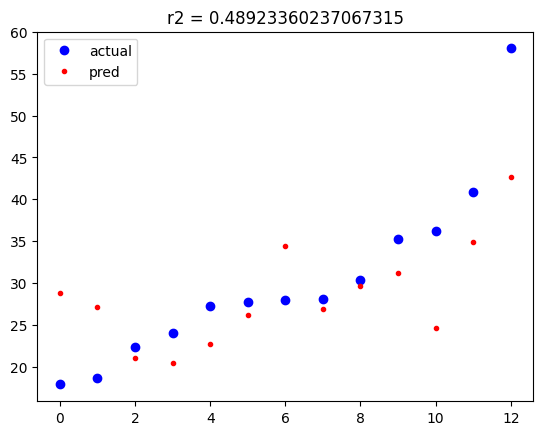
규제를 적용하기 전에는 테스트 데이터의 예측 값은 차이가 매우 큰 것들이 존재했었죠. 워낙 차이가 커서 테스트 데이터들이 수평선에 있는 것처럼 착각할 정도였습니다.
규제를 적용하니 오차가 있지만 크지 않음을 알 수 있습니다.
물론 학습 데이터의 R2 결정 계수보다는 여전히 낮은 값을 보이고 있습니다.
그렇지만 규제를 적용하기 전에 비하면 많이 나아진 것을 알 수 있습니다.
이처럼 규제를 통해 과적합(오버피팅) 현상을 완화시킬 수 있습니다.
다음은 알파값에 따른 R2 결정 계수를 출력한 코드입니다.
for d in [1,2,3,4]:
print(f"degree={d} =======================")
pf = PolynomialFeatures(degree=d,include_bias=False)
pf.fit(x_train)
x_train_p =pf.transform(x_train)
x_test_p =pf.transform(x_test)
for a in [0.001, 0.01, 0.1, 1, 2, 5, 10]:
print(f"alpha={a} #######")
model = Lasso(alpha=a)
model.fit(x_train_p,y_train)
pred_train = model.predict(x_train_p)
print(f"학습 r2:{r2_score(y_train, pred_train):.4f}")
pred_test = model.predict(x_test_p)
print(f"테스트 r2:{r2_score(y_test, pred_test):.4f}")
print()[out]
degree=1 =======================
alpha=0.001 #######
학습 r2:0.7861
테스트 r2:0.6771
alpha=0.01 #######
학습 r2:0.7860
테스트 r2:0.6817
alpha=0.1 #######
학습 r2:0.7800
테스트 r2:0.7031
alpha=1 #######
학습 r2:0.7748
테스트 r2:0.7446
alpha=2 #######
학습 r2:0.7668
테스트 r2:0.7596
alpha=5 #######
학습 r2:0.7660
테스트 r2:0.7523
alpha=10 #######
학습 r2:0.7632
테스트 r2:0.7421
degree=2 =======================
alpha=0.001 #######
학습 r2:0.8321
테스트 r2:0.2435
alpha=0.01 #######
학습 r2:0.8293
테스트 r2:0.1238
alpha=0.1 #######
학습 r2:0.8233
테스트 r2:0.2528
alpha=1 #######
학습 r2:0.7943
테스트 r2:0.7066
alpha=2 #######
학습 r2:0.7863
테스트 r2:0.7393
alpha=5 #######
학습 r2:0.7851
테스트 r2:0.7446
alpha=10 #######
학습 r2:0.7848
테스트 r2:0.7489
degree=3 =======================
alpha=0.001 #######
학습 r2:0.8498
테스트 r2:0.5072
alpha=0.01 #######
학습 r2:0.8503
테스트 r2:0.3512
alpha=0.1 #######
학습 r2:0.8500
테스트 r2:0.1851
alpha=1 #######
학습 r2:0.8489
테스트 r2:-0.1619
alpha=2 #######
학습 r2:0.8471
테스트 r2:-0.3076
alpha=5 #######
학습 r2:0.8442
테스트 r2:-0.1759
alpha=10 #######
학습 r2:0.8423
테스트 r2:-0.1041
degree=4 =======================
alpha=0.001 #######
학습 r2:0.8678
테스트 r2:0.6138
alpha=0.01 #######
학습 r2:0.8686
테스트 r2:0.5858
alpha=0.1 #######
학습 r2:0.8666
테스트 r2:0.5236
alpha=1 #######
학습 r2:0.8644
테스트 r2:0.2607
alpha=2 #######
학습 r2:0.8627
테스트 r2:0.0716
alpha=5 #######
학습 r2:0.8617
테스트 r2:0.0708
alpha=10 #######
학습 r2:0.8605
테스트 r2:0.0301테스트 데이터의 예측 R2 결정 계수는 특성을 변환하기 않은(1차) 상태에서 규제를 2를 주었을 때 0.7596으로 제일 좋네요.
이 때의 학습 데이터의 예측 R2 결정 계수는 0.7668로 큰 차이가 없음을 알 수 있습니다.
물론 모델을 평가할 때 이 둘의 차이를 좁히는 것이 목표는 아닙니다.
실제 목표는 학습에 사용하지 않은 데이터의 예측 결과가 좋아야 하는 것이죠. 결국 테스트 데이터로 모델을 평가했을 때 좋은 결과를 내야 하는 거입니다.
리지와 엘라스틱 넷에서 실험
리지와 엘라스틱 넷에 관한 실험도 라쏘 모델과 같습니다.
여기에서는 시각화 과정은 생략하고 특성 변환과 알파값에 따른 결과를 확인하는 것으로 할게요.
다음은 리지(Ridge) 모델 실험입니다.
for d in [1,2,3,4]:
print(f"degree={d} =======================")
pf = PolynomialFeatures(degree=d,include_bias=False)
pf.fit(x_train)
x_train_p =pf.transform(x_train)
x_test_p =pf.transform(x_test)
for a in [0.001, 0.01, 0.1, 1, 2, 5, 10]:
print(f"alpha={a} #######")
model = Ridge(alpha=a)
model.fit(x_train_p,y_train)
pred_train = model.predict(x_train_p)
print(f"학습 r2:{r2_score(y_train, pred_train):.4f}")
pred_test = model.predict(x_test_p)
print(f"테스트 r2:{r2_score(y_test, pred_test):.4f}")
print()[out]
degree=1 =======================
alpha=0.001 #######
학습 r2:0.7861
테스트 r2:0.6767
alpha=0.01 #######
학습 r2:0.7861
테스트 r2:0.6773
alpha=0.1 #######
학습 r2:0.7860
테스트 r2:0.6824
alpha=1 #######
학습 r2:0.7834
테스트 r2:0.6951
alpha=2 #######
학습 r2:0.7822
테스트 r2:0.6978
alpha=5 #######
학습 r2:0.7810
테스트 r2:0.7013
alpha=10 #######
학습 r2:0.7804
테스트 r2:0.7053
degree=2 =======================
alpha=0.001 #######
학습 r2:0.8329
테스트 r2:0.3303
alpha=0.01 #######
학습 r2:0.8311
테스트 r2:0.1267
alpha=0.1 #######
학습 r2:0.8297
테스트 r2:0.1016
alpha=1 #######
학습 r2:0.8251
테스트 r2:0.1813
alpha=2 #######
학습 r2:0.8215
테스트 r2:0.2089
alpha=5 #######
학습 r2:0.8165
테스트 r2:0.2668
alpha=10 #######
학습 r2:0.8133
테스트 r2:0.3395
degree=3 =======================
alpha=0.001 #######
학습 r2:0.9405
테스트 r2:-10.8871
alpha=0.01 #######
학습 r2:0.9334
테스트 r2:-3.2386
alpha=0.1 #######
학습 r2:0.9187
테스트 r2:-0.5077
alpha=1 #######
학습 r2:0.8918
테스트 r2:-0.2714
alpha=2 #######
학습 r2:0.8865
테스트 r2:-0.4399
alpha=5 #######
학습 r2:0.8823
테스트 r2:-0.6807
alpha=10 #######
학습 r2:0.8806
테스트 r2:-0.8634
degree=4 =======================
alpha=0.001 #######
학습 r2:0.8808
테스트 r2:-1.2367
alpha=0.01 #######
학습 r2:0.8808
테스트 r2:-1.2367
alpha=0.1 #######
학습 r2:0.8808
테스트 r2:-1.2367
alpha=1 #######
학습 r2:0.8808
테스트 r2:-1.2367
alpha=2 #######
학습 r2:0.8808
테스트 r2:-1.2367
alpha=5 #######
학습 r2:0.8808
테스트 r2:-1.2367
alpha=10 #######
학습 r2:0.8808
테스트 r2:-1.2367리지 모델도 특성은 변환하지 않을 때가 좋네요.
알파값은 10일 때 테스트 R2 결정 계수가 0.7053으로 제일 좋습니다.
다음은 엘라스틱 넷 모델로 실험한 코드입니다.
for d in [1,2,3,4]:
print(f"degree={d} =======================")
pf = PolynomialFeatures(degree=d,include_bias=False)
pf.fit(x_train)
x_train_p =pf.transform(x_train)
x_test_p =pf.transform(x_test)
for a in [0.001, 0.01, 0.1, 1, 2, 5, 10]:
print(f"alpha={a} #######")
model = ElasticNet(alpha=a)
model.fit(x_train_p,y_train)
pred_train = model.predict(x_train_p)
print(f"학습 r2:{r2_score(y_train, pred_train):.4f}")
pred_test = model.predict(x_test_p)
print(f"테스트 r2:{r2_score(y_test, pred_test):.4f}")
print()[out]
degree=1 =======================
alpha=0.001 #######
학습 r2:0.7861
테스트 r2:0.6781
alpha=0.01 #######
학습 r2:0.7855
테스트 r2:0.6871
alpha=0.1 #######
학습 r2:0.7808
테스트 r2:0.7015
alpha=1 #######
학습 r2:0.7777
테스트 r2:0.7309
alpha=2 #######
학습 r2:0.7731
테스트 r2:0.7499
alpha=5 #######
학습 r2:0.7665
테스트 r2:0.7568
alpha=10 #######
학습 r2:0.7652
테스트 r2:0.7486
degree=2 =======================
alpha=0.001 #######
학습 r2:0.8302
테스트 r2:0.1061
alpha=0.01 #######
학습 r2:0.8287
테스트 r2:0.1399
alpha=0.1 #######
학습 r2:0.8186
테스트 r2:0.2596
alpha=1 #######
학습 r2:0.8001
테스트 r2:0.6441
alpha=2 #######
학습 r2:0.7930
테스트 r2:0.7136
alpha=5 #######
학습 r2:0.7852
테스트 r2:0.7422
alpha=10 #######
학습 r2:0.7851
테스트 r2:0.7446
degree=3 =======================
alpha=0.001 #######
학습 r2:0.8500
테스트 r2:0.4249
alpha=0.01 #######
학습 r2:0.8504
테스트 r2:0.3605
alpha=0.1 #######
학습 r2:0.8503
테스트 r2:0.2434
alpha=1 #######
학습 r2:0.8498
테스트 r2:0.0379
alpha=2 #######
학습 r2:0.8490
테스트 r2:-0.1831
alpha=5 #######
학습 r2:0.8463
테스트 r2:-0.2880
alpha=10 #######
학습 r2:0.8440
테스트 r2:-0.1710
degree=4 =======================
alpha=0.001 #######
학습 r2:0.8692
테스트 r2:0.5915
alpha=0.01 #######
학습 r2:0.8683
테스트 r2:0.5787
alpha=0.1 #######
학습 r2:0.8665
테스트 r2:0.5602
alpha=1 #######
학습 r2:0.8648
테스트 r2:0.3318
alpha=2 #######
학습 r2:0.8643
테스트 r2:0.2532
alpha=5 #######
학습 r2:0.8625
테스트 r2:0.0910
alpha=10 #######
학습 r2:0.8617
테스트 r2:0.0695
특성 변환을 하지 않고 알파값이 5일 때 테스트 R2 결정 계수가 0.7568로 제일 좋네요.
마지막으로 비교를 위해 규제를 적용하기 전 점수를 확인해 볼게요.
for d in [1,2,3,4]:
print(f"degree={d} =======================")
pf = PolynomialFeatures(degree=d,include_bias=False)
pf.fit(x_train)
x_train_p =pf.transform(x_train)
x_test_p =pf.transform(x_test)
model = LinearRegression()
model.fit(x_train_p,y_train)
pred_train = model.predict(x_train_p)
print(f"학습 r2:{r2_score(y_train, pred_train):.4f}")
pred_test = model.predict(x_test_p)
print(f"테스트 r2:{r2_score(y_test, pred_test):.4f}")
print()[out]
degree=1 =======================
학습 r2:0.7861
테스트 r2:0.6766
degree=2 =======================
학습 r2:0.8335
테스트 r2:0.5068
degree=3 =======================
학습 r2:0.9967
테스트 r2:-263.9885
degree=4 =======================
학습 r2:1.0000
테스트 r2:-414.7134규제를 적용하기 전의 테스트 R2 결정 계수도 특성 변환하기 않았을 때 0.6766으로 제일 높은 점수가 나오고 있습니다.
특히 규제를 적용하기 전에는 특성 변환의 차원 수가 높을 수록 오버피팅 현상이 뚜렷해 지는 것을 알 수 있죠.
결론적으로 규제를 통해 오버피팅 현상을 줄일 수 있음을 확인하였습니다.
본 실험에서는 Lasso 모델로 특성을 변환하지 않고 알파값을 2를 주었을 때 가장 좋은 결과를 도출함을 알 수 있습니다.
